题目内容
【题目】直线MN与直线PQ垂直相交于O，点A在直线PQ上运动，点B在直线MN上运动．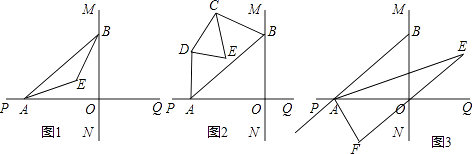 
（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．
（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．
（3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．
【答案】
（1）解：∠AEB的大小不变，
∵直线MN与直线PQ垂直相交于O，
∴∠AOB=90°，
∴∠OAB+∠OBA=90°，
∵AE、BE分别是∠BAO和∠ABO角的平分线，
∴∠BAE= 
∠OAB，∠ABE= ∠ABO，
∴∠BAE+∠ABE= （∠OAB+∠ABO）=45°，
∴∠AEB=135°；
（2）解：∠CED的大小不变．
延长AD、BC交于点F．
∵直线MN与直线PQ垂直相交于O，
∴∠AOB=90°，
∴∠OAB+∠OBA=90°，
∴∠PAB+∠MBA=270°，
∵AD、BC分别是∠BAP和∠ABM的角平分线，
∴∠BAD= ∠BAP，∠ABC= ∠ABM，
∴∠BAD+∠ABC= （∠PAB+∠ABM）=135°，
∴∠F=45°，
∴∠FDC+∠FCD=135°，
∴∠CDA+∠DCB=225°，
∵DE、CE分别是∠ADC和∠BCD的角平分线，
∴∠CDE+∠DCE=112.5°，
∴∠E=67.5°；
（3）解：（3）∵∠BAO与∠BOQ的角平分线相交于E，
∴∠EAO= ∠BAO，∠EOQ= ∠BOQ，
∴∠E=∠EOQ﹣∠EAO= （∠BOQ﹣∠BAO）= ∠ABO，
∵AE、AF分别是∠BAO和∠OAG的角平分线，
∴∠EAF=90°．
在△AEF中，
∵有一个角是另一个角的3倍，故有：
①∠EAF=3∠E，∠E=30°，∠ABO=60°；
②∠EAF=3∠F，∠E=60°，∠ABO=120°；
③∠F=3∠E，∠E=22.5°，∠ABO=45°；
④∠E=3∠F，∠E=67.5°，∠ABO=135°．
∴∠ABO为60°或45°．
【解析】（1）根据直线MN与直线PQ垂直相交于O可知∠AOB=90°，再由AE、BE分别是∠BAO和∠ABO角的平分线得出∠BAE= ∠OAB，∠ABE= ∠ABO，由三角形内角和定理即可得出结论；（2）延长AD、BC交于点F，根据直线MN与直线PQ垂直相交于O可得出∠AOB=90°，进而得出∠OAB+∠OBA=90°，故∠PAB+∠MBA=270°，再由AD、BC分别是∠BAP和∠ABM的角平分线，可知∠BAD= ∠BAP，∠ABC= ∠ABM，由三角形内角和定理可知∠F=45°，再根据DE、CE分别是∠ADC和∠BCD的角平分线可知∠CDE+∠DCE=112.5°，进而得出结论；（3）由∠BAO与∠BOQ的角平分线相交于E可知∠EAO= ∠BAO，∠EOQ= ∠BOQ，进而得出∠E的度数，由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°，在△AEF中，由一个角是另一个角的3倍分四种情况进行分类讨论．
【考点精析】本题主要考查了三角形的“三线”和三角形的内角和外角的相关知识点，需要掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部，是三角形内切圆的圆心，称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部，是三角形的几何中心，称为中心);3、三角形的高线是顶点到对边的距离；注意：三角形的中线和角平分线都在三角形内；三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题．
