Question

【题目】我们定义：

在一个三角形中，如果一个角的度数是另一个角的度数倍，那么这样的三角形我们称之为“和谐三角形”.如：三个内角分别为，，的三角形是“和谐三角形”

概念理解：

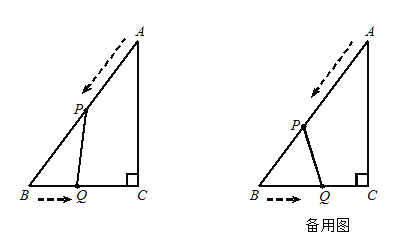
如图，，在射线上找一点，过点作交于点，以为端点作射线，交线段于点（点不与重合）

（1）的度数为 ， （填“是”或“不是”）“和谐三角形”

（2）若，求证：是“和谐三角形”.

应用拓展：

如图，点在的边上，连接，作的平分线交于点，在上取点，使，.若是“和谐三角形”，求的度数.

Answer 1

【答案】（1）°，是；（2）见解析；（3）或

【解析】

（1）根据垂直的定义、三角形内角和定理求出∠ABO的度数，根据“和谐三角形”的概念判断；

（2）根据三角形外角的性质求出的度数，然后根据“和谐三角形”的概念证明即可；

应用拓展：首先易证∠EFC＝∠ADC，根据平行线的性质得到∠DEF＝∠ADE，推出DE∥BC，得到∠CDE＝∠BCD，根据角平分线的定义得到∠ADE＝∠CDE，求得∠B＝∠BCD，然后根据“和谐三角形”的定义求解即可．

解： (1)∵,

∴,

∴,

∵,

∴为“和谐三角形”,

故答案为：°；是；

(2)证明：∵,,

∵,

∴,

∵,

∴是“和谐三角形”；

应用拓展：

∵,,

∴,

∴,

∴,

∵,

∴

∴,

∴,

∵平分,

∴,

∴,

∵是“和谐三角形”,

∴,或,

∵,

∴或.