题目内容
【题目】如图(1),AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图(2),∠BDC的平分线分别交AC,BC于点E,F,求∠CEF的度数.

【答案】(1)见解析;(2)45°.
【解析】试题分析:(1)连接OC,根据切线的性质和直径所对的圆周角是直角得出∠DCO=∠ACB=90°,然后根据等角的余角相等即可得出结论;
(2)根据三角形的外角的性质证明∠CEF=∠CFE即可求解.
试题解析:
(1)证明:如图1中,连接OC.
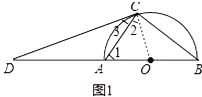
∵OA=OC,∴∠1=∠2,
∵CD是⊙O切线,∴OC⊥CD,
∴∠DCO=90°,∴∠3+∠2=90°,
∵AB是直径,∴∠1+∠B=90°,
∴∠3=∠B.
(2)解:∵∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,
∵∠CDE=∠FDB,∠ECD=∠B,∴∠CEF=∠CFE,
∵∠ECF=90°,
∴∠CEF=∠CFE=45°.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目

