题目内容
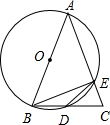
如图所示,在△ABC中,AB=4
,AC=6,BC=2
,P是AC上与A、C不重合的一个动点,过P、B、C的⊙O交AB于D.设PA=x,PC2+PD2=y,求y与x的函数关系式,并确定x的取值范围.

| 3 |
| 3 |

∵AB=4
,AC=6,BC=2
,
∴AB2=(4
)2=48,AC2=62=36,BC2=(2
)2=12,
∴AB2=AC2+BC2,
∴△ABC为直角三角形,且∠A=30°,
连接PB,则PB为⊙O的直径,
∴PD⊥AB,
∵在Rt△APD中,∠A=30°,PA=x,
∴PD=
x,
∴y=PC2+PD2=(6-x)2+(
)2=
x2-12x+36(0<x<6).

| 3 |
| 3 |
∴AB2=(4
| 3 |
| 3 |
∴AB2=AC2+BC2,
∴△ABC为直角三角形,且∠A=30°,
连接PB,则PB为⊙O的直径,
∴PD⊥AB,
∵在Rt△APD中,∠A=30°,PA=x,
∴PD=
| 1 |
| 2 |
∴y=PC2+PD2=(6-x)2+(
| x |
| 2 |
| 5 |
| 4 |


练习册系列答案
相关题目