题目内容
【题目】在
中，
的平分线
与外角
的平分线
所在的直线交于点
.
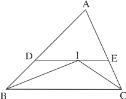
（1）如图1，若
，求
的度数；
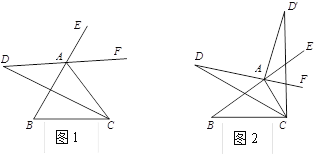
（2）如图2，把
沿
翻折，点落在
处.
①当
时，求
的度数；②试确定
与的数量关系，并说明理由.
【答案】（1）30°；（2）①90°；②
，理由详见解析.
【解析】
（1）已知
平分
、
平分
，根据角平分线的定义可得
、
，根据三角形外角的性质可得
、
，由此可得
；（2）①已知
，由垂直的定义可得
；已知
沿
翻折得到
，由折叠的性质可
；由平角的定义及角平分线的定义可得
、
，所以
，即可求得
；②，设
，已知沿翻折得到，由折叠的性质可得
，由平角的定义可得
，再由角平分线的定义可得
，所以
，再由平角的定义可得
，即可证得.
解：（1）∵平分
∴
∵平分
∴
∵，
∴
（2）①∵
∴
∵沿翻折得到
∴
∴，
∴
∴
②，理由如下：
设
∵
沿
翻折得到
∴
∴
∴
∴
∴
即：
练习册系列答案
名校课堂系列答案
相关题目
