题目内容
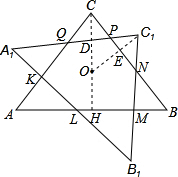
如图,△ABC是等腰三角形,∠C=90°,O是△ABC内一点,点O到△ABC各边的距离等于1,将△ABC绕点O顺时针旋转45°得到△A1B1C1,两三角形的公共部分为多边形KLMNPQ.
①证明:△AKL,△BMN,△CPQ都是等腰直角三角形.
②求证:△ABC与△A1B1C1公共部分的面积.

①证明:△AKL,△BMN,△CPQ都是等腰直角三角形.
②求证:△ABC与△A1B1C1公共部分的面积.

证明:①连接OC、OC1,分别交PQ、NP于点D、E,根据题意得∠COC1=45°.
∵点O到AC和BC的距离都等于1,
∴OC是∠ACB的平分线.
∵∠ACB=90°∴∠OCE=∠OCQ=45°
同理∠OC1D=∠OC1N=45°
∴∠OEC=∠ODC1=90°
∴∠CQP=∠CPQ=∠C1PN=∠C1NP=45°
∴△CPQ和△C1NP都是等腰直角三角形.
∴∠BNM=∠C1NP=45°∠A1QK=∠CQP=45°,
∵∠B=45°∠A1=45°,
∴△BMN和△A1KQ都是等腰直角三角形.
∴∠B1ML=∠BMN=90°,∠AKL=∠A1KQ=90°
∴∠B1=45°∠A=45°
∴△B1ML和△AKL也都是等腰直角三角形.
②在Rt△ODC1和Rt△OEC中,
∵OD=OE=1,∠COC1=45°
∴OC=OC1=
∴CD=C1E=
-1
∴PQ=NP=2(
-1)=2
-2,CQ=CP=C1P=C1N=
(
-1)=2-
∴S△CPQ=
×(2-
)2=3-2
延长CO交AB于H
∵CO平分∠ACB,且AC=BC
∴CH⊥AB,
∴CH=CO+OH=
+1
∴AC=BC=A1C1=B1C1=
(
+1)=2+
,
∴S△ABC=
×(2+
)2=3+2
,
∵A1Q=BN=(2+
)-(2
-2)-(2-
)=2,
∴KQ=MN=
=
,
∴S△BMN=
×(
)2=1,
∵AK=(2+
)-(2-
)-
=
,
∴S△AKL=
×(
)2=1,
∵点O到AC和BC的距离都等于1,
∴OC是∠ACB的平分线.
∵∠ACB=90°∴∠OCE=∠OCQ=45°
同理∠OC1D=∠OC1N=45°
∴∠OEC=∠ODC1=90°
∴∠CQP=∠CPQ=∠C1PN=∠C1NP=45°
∴△CPQ和△C1NP都是等腰直角三角形.
∴∠BNM=∠C1NP=45°∠A1QK=∠CQP=45°,
∵∠B=45°∠A1=45°,
∴△BMN和△A1KQ都是等腰直角三角形.
∴∠B1ML=∠BMN=90°,∠AKL=∠A1KQ=90°
∴∠B1=45°∠A=45°
∴△B1ML和△AKL也都是等腰直角三角形.
②在Rt△ODC1和Rt△OEC中,
∵OD=OE=1,∠COC1=45°
∴OC=OC1=
| 2 |
∴CD=C1E=
| 2 |
∴PQ=NP=2(
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴S△CPQ=
| 1 |
| 2 |
| 2 |
| 2 |
延长CO交AB于H
∵CO平分∠ACB,且AC=BC
∴CH⊥AB,
∴CH=CO+OH=
| 2 |
∴AC=BC=A1C1=B1C1=
| 2 |
| 2 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 2 |
| 2 |
∵A1Q=BN=(2+
| 2 |
| 2 |
| 2 |
∴KQ=MN=
| 2 | ||
|
| 2 |
∴S△BMN=
| 1 |
| 2 |
| 2 |
∵AK=(2+
| 2 |
| 2 |
| 2 |
| 2 |
∴S△AKL=
| 1 |
| 2 |
| 2 |
|


练习册系列答案
相关题目
 1、V2的两个图形,且
1、V2的两个图形,且