题目内容
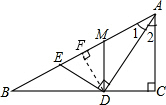
如图，Rt△ABC中，AC⊥BC，AD平分∠BAC交BC于点D，DE⊥AD交AB于点E，M为AE中点，连接MD，若BD=2，CD=1．则MD的长为______．
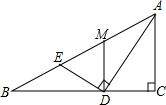
过点D作DF⊥AB于点F．
∵AD平分∠BAC交BC于点D，CD=1，
∴FD=CD=1；
在Rt△BDF中，FD=1，BD=2，
∴∠B=30°（30°角所对的直角边是斜边的一半）；
∴∠1=∠2=30°，
∴在Rt△AFD中，AD=2FD=2；
∴在Rt△AED中，AE=
，
∴MD=
AE=
．
故答案是：
．
∵AD平分∠BAC交BC于点D，CD=1，
∴FD=CD=1；
在Rt△BDF中，FD=1，BD=2，
∴∠B=30°（30°角所对的直角边是斜边的一半）；
∴∠1=∠2=30°，
∴在Rt△AFD中，AD=2FD=2；
∴在Rt△AED中，AE=
4
| ||
| 3 |
∴MD=
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
故答案是：
| 2 |
| 3 |
| 3 |
练习册系列答案
名校课堂系列答案
相关题目
