题目内容
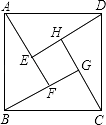
【题目】如图,Rt△ACB中,∠ACB=90°,∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD﹣AH=AB;④DG=AP+GH.其中正确的是( )

A. ①②③ B. ①②④ C. ②③④ D. ①②③④
【答案】A
【解析】
①根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠CAP,再根据角平分线的定义![]() 然后利用三角形的内角和定理整理即可得解;
然后利用三角形的内角和定理整理即可得解;
②③先根据直角的关系求出![]() ,然后利用角角边证明△AHP与△FDP全等,根据全等三角形对应边相等可得
,然后利用角角边证明△AHP与△FDP全等,根据全等三角形对应边相等可得![]() ,对应角相等可得
,对应角相等可得![]() 然后利用平角的关系求出
然后利用平角的关系求出![]() ,再利用角角边证明△ABP与△FBP全等,然后根据全等三角形对应边相等得到
,再利用角角边证明△ABP与△FBP全等,然后根据全等三角形对应边相等得到![]() ,从而得解;
,从而得解;
④根据PF⊥AD,∠ACB=90°,可得AG⊥DH,然后求出∠ADG=∠DAG=45°,再根据等角对等边可得DG=AG,再根据等腰直角三角形两腰相等可得GH=GF,然后求出DG=GH+AF,有直角三角形斜边大于直角边,AF>AP,从而得出本小题错误.
①∵∠ABC的角平分线BE和∠BAC的外角平分线,
∴![]()
![]()
在△ABP中,![]()
![]()
![]()
![]() ,故本小题正确;
,故本小题正确;
②③∵![]()
∴![]()
∴∠AHP=∠FDP,
∵PF⊥AD,
∴![]()
在△AHP与△FDP中,

∴△AHP≌△FDP(AAS),
∴DF=AH,
∵AD为∠BAC的外角平分线,∠PFD=∠HAP,
∴![]()
又∵![]()
∴∠PAE=∠PFD,
∵∠ABC的角平分线,
∴∠ABP=∠FBP,
在△ABP与△FBP中,

∴△ABP≌△FBP(AAS),
∴AB=BF,AP=PF故②小题正确;
∵BD=DF+BF,
∴BD=AH+AB,
∴BDAH=AB,故③小题正确;
④∵PF⊥AD,![]()
∴AG⊥DH,
∵AP=PF,PF⊥AD,
∴![]()
∴![]()
∴DG=AG,
∵![]() AG⊥DH,
AG⊥DH,
∴△ADG与△FGH都是等腰直角三角形,
∴DG=AG,GH=GF,
∴DG=GH+AF,
∵AF>AP,
∴DG=AP+GH不成立,故本小题错误,
综上所述①②③正确。
故选A.

【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?