题目内容
【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系: ;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC= 时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是 .
【答案】
(1)ED=EC
(2)
DE是⊙O的切线.理由如下:
连接OD,如图,
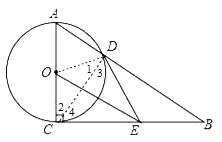
∵BC为切线,
∴OC⊥BC,∴∠OCB=90°,即∠2+∠4=90°,
∵OC=OD,ED=EC,
∴∠1=∠2,∠3=∠4,
∴∠1+∠3=∠2+∠4=90°,即∠ODE=90°,
∴OD⊥DE,∴DE 是⊙O 的切线;
(3)2;正方形
【解析】(1)连接CD,如图,
∵AC是⊙O的直径,∴∠ADC=90°,
∵E是BC的中点,∴ED=EC=BE.
3)当BC=2 时, ∵CA=CB=2,
∴CE=DE=1 , OC=OD=1,
又∵OC⊥CE,∴四边形 ODEC为正方形.
∴AO=DE=1,且 AO∥DE,∴四边形AOED是平行四边形.
(1)根据直径所对的圆周角是90度,可得CD⊥AB,由E是BC的中点,可得斜边上的中线等于斜边的一半;(2)根据等边对等角,通过角的等量代换可得∠ODE=90°;(3)要使四边形AOED是平行四边形,则对边相等且平行,即DE=OA=1,则BC=2DE=2,此时OC=OD=CE=DE=1,且OC⊥CE,则四边形ODEC为正方形.

练习册系列答案
相关题目







