Question

【题目】在⊙O中，AB为直径，点P在AB的延长线上，PC与⊙O相切于点C，点D为弧AC上的点，且2∠DAB﹣∠P＝90°，连接AD．

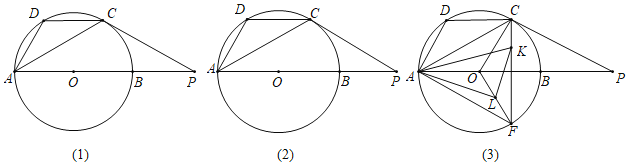
（1）如图1，求证：弧AD＝弧BC；

（2）如图2，PC＝6，PB＝，求∠ADC度数；

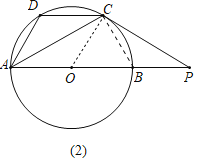
（3）如图3，在（2）的条件下，F为AB下方⊙O上一点．∠ACF＝60°，L为OF中点，LK⊥AL于L，交CF于点K．连接AK，求AK的长．

Answer 1

【答案】（1）见解析；（2）∠ADC＝120°；（3）AK＝2．

【解析】

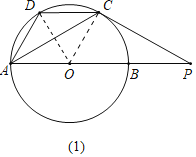
（1）如图1中，连接OD，OC．想办法证明∠AOD＝∠COB即可．

（2）利用相似三角形的性质求出PA，再证明∠COB＝60°即可解决问题．

（3）如图3中，作LH⊥AB于H，设KL交AP于N．CF交AB于M．首先证明△ACF是等边三角形，解直角三角形求出OH，HL，HN，利用相似三角形的性质求出KM，再利用勾股定理即可解决问题．

（1）证明：如图1中，连接OD，OC．

∵PC是⊙O的切线，

∴OC⊥PC，

∴∠PCO＝90°，

∴∠P+∠POC＝90°，

∵OA＝OD，

∴∠DAB＝∠ADO，

∵2∠DAB﹣∠P＝90°，

∴180°﹣∠AOD﹣（90°﹣∠POC）＝90°，

∴∠AOD＝∠POC，

∴弧AD＝弧BC．

（2）解：如图2中，连接OC，BC．

∵AB是直径，PC是切线，

∴∠ACB＝∠PCB，

∵OA＝OC，

∴∠OAC＝∠OCA，

∴∠PCB＝∠PAC，

∵∠P＝∠P，

∴△PCB∽△PAC，

∴ ，

∴PC2＝PBPA，

∴PA＝，

∴AB＝PA﹣PB＝4，

∴OC＝OB＝OA＝2，

∴tan∠COB＝ ＝，

∴∠COB＝60°，

∵OC＝OB，

∴△OBC是等边三角形，

∴∠ABC＝60°，

∴∠ADC＝180°﹣∠ABC＝120°．

（3）解：如图3中，作LH⊥AB于H，设KL交AP于N．CF交AB于M．

∵∠AFC＝180°﹣∠ADC＝60°，∠ACF＝60°，

∴△ACF是等边三角形，

由（1）可知，AC＝AF＝CF＝6，∠CAP＝30°，

∵∠CAF＝60°，

∴∠CAN＝∠FAN＝30°，

∴AN⊥CF，

∴CN＝NF＝ AC＝3，

∵OL＝LF＝，

在Rt△OHL中，∠OHL＝90°，∠HOL＝60°，

∴OH＝OL＝ ，HL＝ ，

∵LH∥FN，OL＝LF，

∴OH＝HM＝，

∵AM＝ACcos30°＝6×＝3，HL＝FM＝，

∴

∵AL⊥LK，

∴∠AHL＝∠ALN＝90°，

∵∠LAH＝∠LAN，

∴△AHL∽△ALN，

∴，

∴，

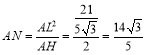∴HN＝AN﹣AH＝，NM＝HM﹣HN＝，

∵HL∥KM，

∴，

∴，

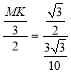∴MK＝1，

∴AK＝