题目内容
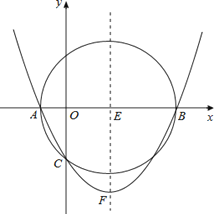
【题目】如图，在平面直角坐标系中，抛物线经过点
、
、
．
（1）求抛物线的解析式；
（2）若
与抛物线的对称轴交于点
，以
为圆心，
长为半径作圆，
与
轴的位置关系如何？请说明理由．
（3）过点作的切线
，交
轴于点
，请求出直线的解析式及点坐标．
【答案】（1）y＝﹣
x2﹣x+4；（2）⊙A与y轴的位置关系是相交，理由见解析；（3）直线GE的表达式为：y＝﹣
x+
，G（
，0）．
【解析】
（1）根据待定系数法，即可求解；
（2）根据待定系数法，求出直线AC的表达式为：y＝
x+4，进而求出点E的坐标，可得AE的长，比较AE与AO的大小关系，即可得到结论；
（3）由直线AC的表达式为：y＝x+4，结合AC⊥EG，可得直线EG的表达式为：y＝﹣x+m，结合点E的坐标，可得直线GE的表达式，进而即可求解．
（1）∵抛物线经过点
、
，
∴设二次函数的表达式为：y＝a（x+3）（x﹣2）＝a（x2+x﹣6），
把C(0，4)代入得：﹣6a＝4，解得：a＝﹣，
∴抛物线的表达式为：y＝﹣x2﹣x+4；
（2）⊙A与y轴的位置关系是相交，理由如下：
设直线AC的解析式为y＝kx+b，
将点A、C的坐标代入一次函数表达式：y＝kx+b得：
，解得：
，
∴直线AC的表达式为：y＝x+4，
∵抛物线的对称轴为：直线x＝﹣
，
∴当x＝﹣时，y＝
∴点E(﹣，)，
∴AE＝
＝
＞AO，
∴⊙A与y轴的位置关系是相交；
（3）直线AC的表达式为：y＝x+4，
∵
是
的切线，切点是点E，
∴AC⊥EG，
∴设直线EG的表达式为：y＝﹣x+m，
将点E的坐标代入上式，得＝﹣×(﹣)+m，解得：m＝，
∴直线GE的表达式为：y＝﹣x+，
∵当y＝0时，x＝，
∴点G(，0)．
【题目】为了丰富校园文化，某学校决定举行学生趣味运动会，将比赛项目确定为袋鼠跳、夹球跑、跳大绳、绑腿跑和拔河赛五种．为了解学生对这五项运动的喜欢情况，随机调查了该校a名学生最喜欢的一种项目（每名学生必选且只能选择五项中的一种）并将调查结果绘制成如下不完整的统计图表：
学生最喜欢的活动项目的人数统计表 | ||
项目 | 学生数（名） | 百分比（%） |
袋鼠跳 | 45 | 15 |
夹球跑 | 30 | c |
跳大绳 | 75 | 25 |
绑腿跑 | b | m |
拔河赛 | 90 | 30 |
根据图表中提供的信息，解答下列问题：
（1）a＝ ，b＝ ，c＝ ；
（2）请将条形统计图补充完整；
（3）根据调查结果，请你估计该校3000名学生中有多少名学生最喜欢绑腿跑．
【题目】已知二次函数
的
与
的部分对应值如下表：
| -1 | 0 | 2 | 3 | 4 |
| 5 | 0 | -4 | -3 | 0 |
下列结论：①抛物线开口向上；②抛物线的对称轴为直线
；③当
时，
；④抛物线与轴的两个交点间的距离是4；⑤若
，
是抛物线上两点，则
，其中正确的结论是_______．
