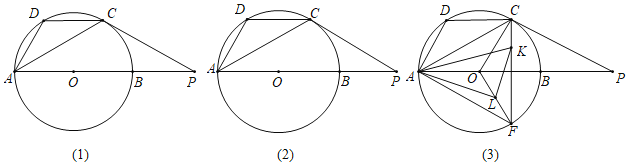
题目内容
【题目】如图,在矩形ABCD中,tan∠ACB=![]() ,将其沿对角线AC剪开得到△ABC和△ADE(点C与点E重合),将△ADE绕点A旋转,当线段AD与AB在同一条直线上时,连接EC,则∠ECB的正切值为_____.
,将其沿对角线AC剪开得到△ABC和△ADE(点C与点E重合),将△ADE绕点A旋转,当线段AD与AB在同一条直线上时,连接EC,则∠ECB的正切值为_____.

【答案】![]() 或3
或3
【解析】
分两种情况:①由三角函数定义求出BC=2AB,由旋转的性质得出AD'=AD=2AB=2BD',D'E=DE=AB,∠AD'E=90°,证明△BCF∽△D'EF,得出![]() =2,
=2,
求出BF=![]() BD'=
BD'=![]() BC,由三角函数定义即可得出答案;
BC,由三角函数定义即可得出答案;
①作EG⊥BC于G,交AD于F,则EG=D'B=3AB,D'E=BG=AB,得出CG=BG=AB,由三角函数定义即可得出答案.
分两种情况:
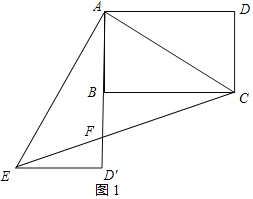
①如图1所示:
∵四边形ABCD是矩形,
∴AD=BC,∠D=∠ABC=90°,
∵tan∠ACB=![]() ,
,
∴BC=2AB,
由旋转的性质得:AD'=AD=2AB=2BD',D'E=DE=AB,∠AD'E=90°,
∴D'E∥BC,
∴△BCF∽△D'EF,

∴![]() =2,
=2,
∴BF=![]() BD'=
BD'=![]() BC,
BC,
∴∠ECB的正切值=![]() ;
;
①如图2所示:作EG⊥BC于G,交AD于F,
则EG=D'B=3AB,D'E=BG=AB,
∴CG=BG=AB,
则∠ECB的正切值=![]() =3;
=3;
综上所述,∠ECB的正切值为![]() 或3;
或3;
故答案为:![]() 或3.
或3.

练习册系列答案
相关题目
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| -1 | 0 | 2 | 3 | 4 |
| 5 | 0 | -4 | -3 | 0 |
下列结论:①抛物线开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④抛物线与
;④抛物线与![]() 轴的两个交点间的距离是4;⑤若
轴的两个交点间的距离是4;⑤若![]() ,
,![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的结论是_______.
,其中正确的结论是_______.