题目内容
【题目】如图，在平面直角坐标系中，坐标原点O是菱形ABCD的对称中心．边AB与x轴平行，点B（1，-2），反比例函数 
（k≠0）的图象经过A，C两点．
（1）求点C的坐标及反比例函数的解析式．
（2）直线BC与反比例函数图象的另一交点为E，求以O，C，E为顶点的三角形的面积．
【答案】
（1）解：连结AC，BD，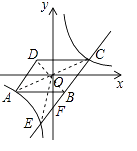
∵坐标原点O是菱形ABCD的对称中心，
∴AC，BD相交于点O，
且∠AOB=90°，
∵B（1，﹣2），且AB∥x轴，
∴设A（a，﹣2），则AO2=a2+4，BO2=5，AB2=（1﹣a）2 ，
在Rt△AOB中，由勾股定理得（1﹣a）2=a2+4+5，解得a=﹣4，
∴A（﹣4，﹣2），∴C（4，2），
∵反比例函数 
（k≠0）的图象经过A，C两点，
∴反比例函数解析式为 
；
（2）解：连结OE，则△OCE是以O，C，E为顶点的三角形，设直线BC的解析式为y=kx+b，
∵点B（1，﹣2），C（4，2）在该直线上，
∴ 
，解得：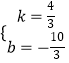 
，
∴直线BC的解析式为 
，设其与y轴交于点F（0， 
），
∵反比例函数为 ，∴ 
，解得x1=4，x2= 
，
∴点E的横坐标为 ，
∴以O，C，E为顶点的三角形的面积= 
= 
．
【解析】（1）连结AC，BD，根据坐标原点O是菱形ABCD的对称中心，可得AC，BD相交于点O，根据菱形的性质得出∠AOB=90°，根据B（1，-2），且AB∥x轴，可设A（a，-2），则AO2=a2+4，BO2=5，AB2=（1-a）2 ， 在Rt△AOB中，由勾股定理可得点A、C的坐标，再根据待定系数法可求反比例函数解析式。
（2）连结OE，则△OCE是以O，C，E为顶点的三角形，利用待定系数法求出直线BC的函数解析式，再求出直线BC与y轴的交点坐标，然后将反比例函数和直线BC联立方程组，求解得出点E的坐标，再根据三角形的面积公式计算即可得出答案。
【考点精析】本题主要考查了确定一次函数的表达式和勾股定理的概念的相关知识点，需要掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．
