题目内容
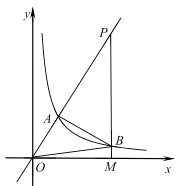
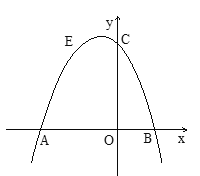
【题目】如图抛物线![]() (a≠0)与x轴的交点为A、B(A在B的左边)且AB=3,与y轴交于C
(a≠0)与x轴的交点为A、B(A在B的左边)且AB=3,与y轴交于C
(1)求A、B两点的坐标.
(2)若抛物线过点E(-1,2),求抛物线的解析式.
(3)在x轴的下方的抛物线上是否存在一点P使得△PAC的面积为3,若存在求出P点的坐标,不存在说明理由.
【答案】(1)A(-2,0)B(1,0);(2)![]() ;(3)存在点P(-3,-4)使△PAC面积为3
;(3)存在点P(-3,-4)使△PAC面积为3
【解析】
(1)由解析式得抛物线对称轴为,又因为A在B的左边且AB=3,即可求出A、B的坐标;
(2)由(1)中的B点坐标结合E点的坐标,即可求得抛物线的解析式;
(3)由题意知,△ABC的面积为3,过B作BM∥AC,交y轴于M,交抛物线于点P,则△PAC面积为3,之后根据相似求得M坐标,再求得BM解析式,联立方程组即可求得答案.
解:(1)由解析式得抛物线对称轴为![]() ,交x轴于D,
,交x轴于D,
又∵AB=3,
∴AD=BD=![]() ,
,
∴AO=2,BO=1,
∴A(-2,0)B(1,0)
(2)把B(1,0)E(-1,2)代入解析式得![]() ,
,
解得![]() ,
,
故抛物线的解析式为![]() ;
;
(3)由(2)中抛物线可知C(0,2),
∴![]() ,
,
过B作BMAC,交y轴于M,交抛物线于点P,

则△PAC面积为3(同底等高),
由△AOC∽△BOM可得OM=1即M(0,-1),
易得直线BM解析式为y=x-1,
联立构成方程组得![]()
解得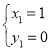 ,
,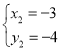
∵点P在x轴下方,
∴存在点P(-3,-4)使△PAC面积为3.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目