题目内容
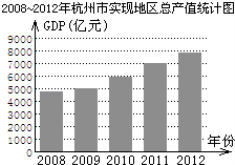
【题目】某企业生成一种节能产品，投放市场供不应求．若该企业每月的产量保持在一定的范围，每套产品的生产成本不高于50万元，每套产品的售价不低于120万元．已知这种产品的月产量x（套）与每套的售价y1（万元）之间满足关系式y1=190﹣2x．月产量x（套）与生成总成本y2（万元）存在如图所示的函数关系．
（1）直接写出y2（2）与x之间的函数关系式；
（2）求月产量x的取值范围；
（3）当月产量x（套）为多少时，这种产品的利润W（万元）最大？最大利润是多少？
【答案】
（1）
解：设y2与x的函数关系式为y2=kx+b，
，得 
，
∴y2与x之间的函数关系式是y2=30x+500
（2）
解：由题意可得，
，
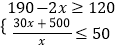解得，25≤x≤35，
即月产量x的取值范围是25≤x≤35
（3）
解：由题意可得，
W=x[190﹣2x﹣ 
]=﹣2（x﹣40）2+2700，
∵25≤x≤35，
∴x=35时，W取得最大值，此时W=2650，
即当月产量x（套）为35套时，这种产品的利润W（万元）最大，最大利润是2650万元．
【解析】（1）根据题意可以设出y2与x之间的函数关系式，然后根据图象中的数据即可求得函数的解析式；（2）根据题意可以列出相应的不等式组，从而可以求得x的取值范围；（3）根据题意可以得到W与x函数关系式，然后化为顶点式，再根据x的取值范围，即可求得W的最大值．
练习册系列答案
相关题目
