Question

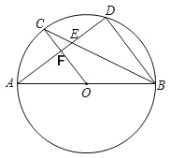
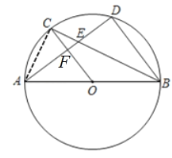
【题目】如图，AB为⊙O的直径，C、D为圆上的两点，OC∥BD，弦AD与BC，OC分别交于E、F

（1）求证：＝；

（2）若CE＝1，EB＝3，求⊙O的半径；

（3）若BD＝6，AB＝10，求D E的长．

Answer 1

【答案】（1）见解析；（2）r=；（3）DE=3

【解析】

（1）由等腰三角形的性质和平行线的性质可得∠OBC＝∠CBD，即可证；

（2）通过证明△ACE∽△BCA，可得，可得AC＝2，由勾股定理可求AB的长，即可求⊙O的半径；

（3）利用勾股定理求得AD＝8，进而求得AF＝DF＝4及OF＝3，结合OC＝OA＝5求得CF＝2，再利用勾股定理分别求得AC＝及BC＝，由相似三角形的性质可得CE＝，进而可求得BE的长，最后再利用勾股定理求得DE长即可．

证明：（1）∵OC＝OB

∴∠OBC＝∠OCB

∵OC∥BD

∴∠OCB＝∠CBD

∴∠OBC＝∠CBD

∴

（2）连接AC，

∵CE＝1，EB＝3，

∴BC＝4

∵

∴∠CAD＝∠ABC，且∠ACB＝∠ACB

∴△ACE∽△BCA

∴

∴AC2＝CBCE＝4×1

∴AC＝2，

∵AB是直径

∴∠ACB＝90°

∴AB＝

∴⊙O的半径为

（3）在Rt△DAB中，AD＝，

∴AF＝DF＝4，

∴OF＝3，

∴CF＝OC-OF＝2，

在Rt△ACF中，AC＝

在Rt△ACB中，BC＝

由（2）AC2＝CECB

得

解得CE＝

∴BE＝BC-CE＝

在Rt△DEB中，DE＝，

∴DE的长为3