Question

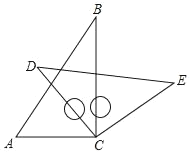
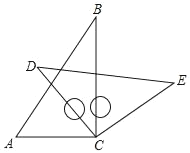
【题目】将一副三角板中的两块直角板中的两个直角顶点重合在一起，即按如图所示的方式叠放在一起，其中∠A＝60°，∠B＝30，∠D＝45°．

（1）若∠BCD＝45°，求∠ACE的度数．

（2）若∠ACE＝150°，求∠BCD的度数．

（3）由（1）、（2）猜想∠ACE与∠BCD存在什么样的数量关系并说明理由．

Answer 1

【答案】（1）∠ACE=135°；（2）∠BCD＝30°；（3）∠ACE与∠BCD互补.理由见解析.

【解析】

（1）先求得∠ACD的度数，即可得到∠ACE的度数；

（2）先求得∠ACD的度数，即可得到∠BCD的度数；

（3）依据∠BCD＝∠ACB﹣∠ACD＝90°﹣∠ACD，∠ACE＝∠DCE+∠ACD＝90°+∠ACD，即可得到∠ACE与∠BCD互补．

解：（1）∵∠BCD＝45°，∠ACB＝90°，

∴∠ACD＝∠ACB﹣∠DCB＝45°，

又∵∠DCE＝90°，

∴∠ACE＝∠ACD+∠DCE＝45°+90°＝135°；

（2）∵∠ACE＝150°，∠DCE＝90°，

∴∠ACD＝∠ACE﹣∠DCE＝150°﹣90°＝60°，

又∵∠ACB＝90°，

∴∠BCD＝∠ACB﹣∠ACD＝90°﹣60°＝30°；

（3）由（1）、（2）猜想∠ACE与∠BCD互补．

理由：∵∠BCD＝∠ACB﹣∠ACD＝90°﹣∠ACD，

∠ACE＝∠DCE+∠ACD＝90°+∠ACD，

∴∠BCD+∠ACE＝90°﹣∠ACD+90°+∠ACD＝180°，

∴∠ACE与∠BCD互补．