题目内容
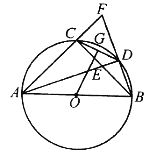
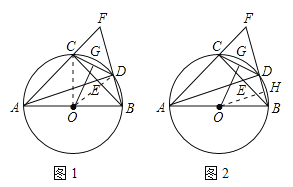
【题目】如图， 
内接于⊙
， 
， 
的平分线
与⊙
交于点
，与
交于点
，延长
，与
的延长线交于点
，连接
， 
是
的中点，连接
.
(1)判断
与
的位置关系，写出你的结论并证明;
(2)求证: 
;
(3)若
，求⊙
的面积.
【答案】（1）OG⊥CD（2）证明见解析（3）6π
【解析】试题分析：（1）根据G是CD的中点，利用垂径定理证明即可；
（2）先证明△ACE与△BCF全等，再利用全等三角形的性质即可证明；
（3）构造等弦的弦心距，运用相似三角形以及勾股定理进行求解．
试题解析：（1）解：猜想OG⊥CD．证明如下：
如图1，连接OC、OD．∵OC=OD，G是CD的中点，∴由等腰三角形的性质，有OG⊥CD．
（2）证明：∵AB是⊙O的直径，∴∠ACB=90°，而∠CAE=∠CBF（同弧所对的圆周角相等）．在Rt△ACE和Rt△BCF中，∵∠ACE=∠BCF=90°，AC=BC，∠CAE=∠CBF，∴Rt△ACE≌Rt△BCF（ASA），∴AE=BF．
（3）解：如图2，过点O作BD的垂线，垂足为H，则H为BD的中点，∴OH=
AD，即AD=2OH，又∠CAD=∠BADCD=BD，∴OH=OG．在Rt△BDE和Rt△ADB中，∵∠DBE=∠DAC=∠BAD，∴Rt△BDE∽Rt△ADB，∴
，即BD2=ADDE，∴
．又BD=FD，∴BF=2BD，∴
①，设AC=x，则BC=x，AB= 
．∵AD是∠BAC的平分线，∴∠FAD=∠BAD．在Rt△ABD和Rt△AFD中，∵∠ADB=∠ADF=90°，AD=AD，∠FAD=∠BAD，∴Rt△ABD≌Rt△AFD（ASA），∴AF=AB= 
，BD=FD，∴CF=AF﹣AC= 
．在Rt△BCF中，由勾股定理，得： 
②，由①、②，得
，∴x2=12，解得： 
或
（舍去），∴
，∴⊙O的半径长为
，∴S⊙O=π（
）2=6π．
