��Ŀ����
��2013���㽭����12�֣���ͼ1����֪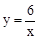 ��x��
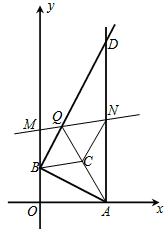
��x�� ��ͼ����һ��P��PA��x���ڵ�A��a��0������B����Ϊ��0��b����b��0��������M��y����������B���Ϸ��ĵ㣬����N������AP�ϣ�����B��AB�Ĵ��ߣ�������AP�ڵ�D����ֱ��MN�ڵ�Q������AQ��ȡAQ���е�ΪC��
��ͼ����һ��P��PA��x���ڵ�A��a��0������B����Ϊ��0��b����b��0��������M��y����������B���Ϸ��ĵ㣬����N������AP�ϣ�����B��AB�Ĵ��ߣ�������AP�ڵ�D����ֱ��MN�ڵ�Q������AQ��ȡAQ���е�ΪC��
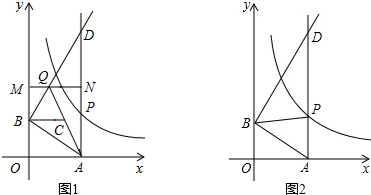
��1����ͼ2������BP�����PAB�������
��2������Q���߶�BD��ʱ�����ı���BQNC�����Σ����Ϊ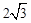 �����ʱP������ꣻ
�����ʱP������ꣻ
��3������Q������BD��ʱ����a=3��b=1�����Ե�B��C��N��QΪ������ı�����ƽ���ı��Σ������ƽ���ı��ε��ܳ���
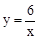 ��x��
��x�� ��ͼ����һ��P��PA��x���ڵ�A��a��0������B����Ϊ��0��b����b��0��������M��y����������B���Ϸ��ĵ㣬����N������AP�ϣ�����B��AB�Ĵ��ߣ�������AP�ڵ�D����ֱ��MN�ڵ�Q������AQ��ȡAQ���е�ΪC��
��ͼ����һ��P��PA��x���ڵ�A��a��0������B����Ϊ��0��b����b��0��������M��y����������B���Ϸ��ĵ㣬����N������AP�ϣ�����B��AB�Ĵ��ߣ�������AP�ڵ�D����ֱ��MN�ڵ�Q������AQ��ȡAQ���е�ΪC��
��1����ͼ2������BP�����PAB�������
��2������Q���߶�BD��ʱ�����ı���BQNC�����Σ����Ϊ
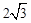 �����ʱP������ꣻ
�����ʱP������ꣻ��3������Q������BD��ʱ����a=3��b=1�����Ե�B��C��N��QΪ������ı�����ƽ���ı��Σ������ƽ���ı��ε��ܳ���
�⣺��1��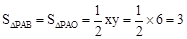 ��
��
��2����ͼ1�����ı���BQNC�����Σ�
��BQ=BC=NQ����BQC=��NQC��
��AB��BQ��C��AQ���е㣬��BC=CQ=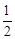 AQ�����BQC=60�㣬��BAQ=30�㡣
AQ�����BQC=60�㣬��BAQ=30�㡣
�ڡ�ABQ�͡�ANQ�У���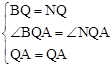 �����ABQ�ա�ANQ��SAS����
�����ABQ�ա�ANQ��SAS����
���BAQ=��NAQ=30�㡣���BAO=30�㡣
��S�ı���BQNC=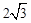 ����BQ=2����AB=
����BQ=2����AB=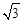 BQ=
BQ=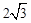 ����OA=
����OA=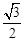 AB=3��
AB=3��
�֡�P���ڷ���������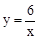 ��ͼ���ϣ���P������Ϊ��3��2����
��ͼ���ϣ���P������Ϊ��3��2����
��3����OB=1��OA=3����AB=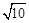 ��
��
�ߡ�AOB�ס�DBA����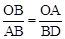 ����BD=3
����BD=3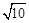 ��
��
����ͼ2������Q���߶�BD�ϣ�
��AB��BD��CΪAQ���е㣬��BC=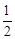 AQ��
AQ��
���ı���BNQC��ƽ���ı��Σ���QN=BC��CN=BQ��CN��BD��
��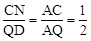 ����BQ=CN=
����BQ=CN=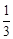 BD=
BD=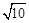 ��
��
��AQ=2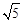 ��
��
��C�ı���BQNC=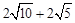 ��
��
����ͼ3������Q���߶�BD���ӳ����ϣ�
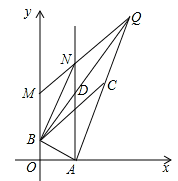
��AB��BD��CΪAQ���е㣬
��BC=CQ=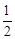 AQ��
AQ��
��ƽ���ı���BNQC�����Σ�BN=CQ��BN��CQ��
��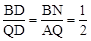 ����BQ=3BD=9
����BQ=3BD=9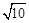 ��
��
��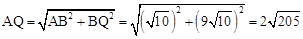 ��
��
��C�ı���BNQC=2AQ=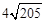 ��
��
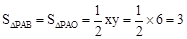 ��
����2����ͼ1�����ı���BQNC�����Σ�
��BQ=BC=NQ����BQC=��NQC��
��AB��BQ��C��AQ���е㣬��BC=CQ=
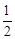 AQ�����BQC=60�㣬��BAQ=30�㡣
AQ�����BQC=60�㣬��BAQ=30�㡣�ڡ�ABQ�͡�ANQ�У���
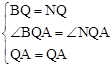 �����ABQ�ա�ANQ��SAS����
�����ABQ�ա�ANQ��SAS�������BAQ=��NAQ=30�㡣���BAO=30�㡣
��S�ı���BQNC=
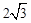 ����BQ=2����AB=
����BQ=2����AB=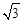 BQ=
BQ=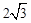 ����OA=
����OA=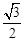 AB=3��
AB=3���֡�P���ڷ���������
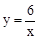 ��ͼ���ϣ���P������Ϊ��3��2����
��ͼ���ϣ���P������Ϊ��3��2������3����OB=1��OA=3����AB=
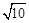 ��
���ߡ�AOB�ס�DBA����
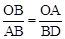 ����BD=3
����BD=3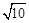 ��
������ͼ2������Q���߶�BD�ϣ�

��AB��BD��CΪAQ���е㣬��BC=
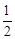 AQ��
AQ�����ı���BNQC��ƽ���ı��Σ���QN=BC��CN=BQ��CN��BD��
��
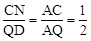 ����BQ=CN=
����BQ=CN=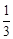 BD=
BD=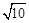 ��
����AQ=2
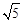 ��
����C�ı���BQNC=
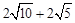 ��
������ͼ3������Q���߶�BD���ӳ����ϣ�

��AB��BD��CΪAQ���е㣬
��BC=CQ=
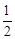 AQ��
AQ����ƽ���ı���BNQC�����Σ�BN=CQ��BN��CQ��
��
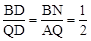 ����BQ=3BD=9
����BQ=3BD=9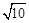 ��
����
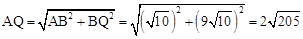 ��
����C�ı���BNQC=2AQ=
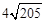 ��
����1������ͬ�ȸߵ����������ε������ȼ��������PAB�������
��2�����������BQC=60�㣬��BAQ=30�㣬Ȼ�����SAS֤����ABQ�ա�ANQ�����������BAO=30�㣬��S�ı���BQNC=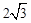 ���OA=3������P�����������
���OA=3������P�����������
��3��������������ۣ�����Q���߶�BD�ϣ���������������AQ�ij�����������ı��ε��ܳ�������Q���߶ο��㣺
BD���ӳ����ϣ���Ȼ��������������AQ�ij����ٽ�һ������ı��ε��ܳ���
��2�����������BQC=60�㣬��BAQ=30�㣬Ȼ�����SAS֤����ABQ�ա�ANQ�����������BAO=30�㣬��S�ı���BQNC=
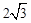 ���OA=3������P�����������
���OA=3������P�������������3��������������ۣ�����Q���߶�BD�ϣ���������������AQ�ij�����������ı��ε��ܳ�������Q���߶ο��㣺
BD���ӳ����ϣ���Ȼ��������������AQ�ij����ٽ�һ������ı��ε��ܳ���

��ϰ��ϵ�д�
�����Ŀ
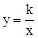 ��ͼ���㣨2����1������k��ֵΪ�� ����
��ͼ���㣨2����1������k��ֵΪ�� ���� ��x��0������D�㣬����D��DC��x�ᣬ����ΪG������OD����֪��AOB�ա�ACD��
��x��0������D�㣬����D��DC��x�ᣬ����ΪG������OD����֪��AOB�ա�ACD��
 ��ͼ���ϵ�һ��,AB��x���ڵ�B,�ҡ�ABO�������3,��k��ֵ��( )
��ͼ���ϵ�һ��,AB��x���ڵ�B,�ҡ�ABO�������3,��k��ֵ��( )
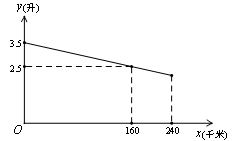
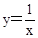 ��x��0����ͼ���ϣ���P1OA1����P2A1A2����P3A2A3��������PnAn��1An���ǵ���ֱ�������Σ�б��OA1��A1A2��A2A3������An��1An����x���ϣ�n�Ǵ��ڻ����2���������������P3��������������������Pn���������������������ú�n��ʽ�ӱ�ʾ����
��x��0����ͼ���ϣ���P1OA1����P2A1A2����P3A2A3��������PnAn��1An���ǵ���ֱ�������Σ�б��OA1��A1A2��A2A3������An��1An����x���ϣ�n�Ǵ��ڻ����2���������������P3��������������������Pn���������������������ú�n��ʽ�ӱ�ʾ����
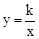 ��һ����������Ϊ��3��4���������ǵ���һ������������
��һ����������Ϊ��3��4���������ǵ���һ������������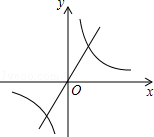
 ����������ͬ�ĵ�A��m��n����m��2����B��p��q����ֱ��y=��x+m+n��y�ύ�ڵ�C�����OBC�����S��ȡֵ��Χ��
����������ͬ�ĵ�A��m��n����m��2����B��p��q����ֱ��y=��x+m+n��y�ύ�ڵ�C�����OBC�����S��ȡֵ��Χ��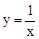 ��y=x��2ͼ��ĺ�����ֱ�Ϊa��b����
��y=x��2ͼ��ĺ�����ֱ�Ϊa��b����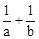 ��ֵΪ�� ����
��ֵΪ�� ����