Question

【题目】如图，在矩形ABCD中，AB=5，BC=3，将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF，点A落在矩形ABCD的边CD上，连接CE，则CE的长是 ．

Answer 1

【答案】
【解析】解：连接AG，

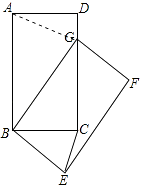
由旋转变换的性质可知，∠ABG=∠CBE，BA=BG=5，BC=BE，由勾股定理得，CG= =4，∴DG=DC﹣CG=1，则AG= = ，∵ ，∠ABG=∠CBE，∴△ABG∽△CBE，∴ ，解得，CE= ，所以答案是： ．

【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案，需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．