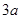题目内容
如图,PA、PB是⊙O的切线,切点分别是A、B,若∠APB=60°,PA=3.则⊙O的半径是 。

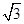 .
.试题分析:连接OA、OP,根据切线长定理即可求得∠OPA=
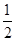 ∠APB,在Rt△OAP中利用三角函数即可求解.
∠APB,在Rt△OAP中利用三角函数即可求解.试题解析:连接OA、OP
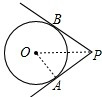
∵PA、PB是⊙O的切线
∴∠OAP=90°,∠APO=
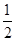 ∠APB=30°
∠APB=30°Rt△OAP中,
∵tan∠APO=
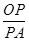 ,
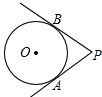
,∴OA=PA•tan30°=
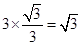
考点: 切线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
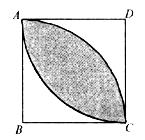
 ,
, ,则
,则 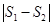 =_________(平方单位).
=_________(平方单位).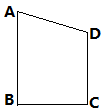
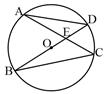
 的弦,
的弦, ,C是优弧AB上的一点,BD//OA,交CA的延长线于点D,连接BC。
,C是优弧AB上的一点,BD//OA,交CA的延长线于点D,连接BC。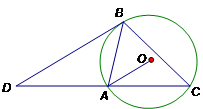
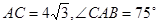 ,求⊙
,求⊙
 .
.
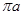 B.
B. 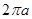 C.
C. 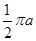 D.
D.