题目内容
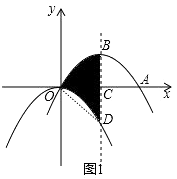
【题目】如图(1),抛物线 y=﹣ ![]() x2平移后过点A(8,0)和原点,顶点为B,对称轴与x轴相交于点C,与原抛物线相交于点D.
x2平移后过点A(8,0)和原点,顶点为B,对称轴与x轴相交于点C,与原抛物线相交于点D.
(1)求平移后抛物线的解析式及点D的坐标;
(2)直接写出阴影部分的面积 S阴影;
(3)如图(2),直线AB与y轴相交于点P,点M为线段OA上一动点(点M不与点A,O重合 ),∠PMN为直角,MN与AP相交于点N,设OM=t,试探究:t为何值时,△MAN为等腰三角形?
【答案】
(1)
解:平移后的抛物线解析式为y=﹣ ![]() x(x﹣8),
x(x﹣8),
即y=﹣ ![]() x2+
x2+ ![]() x
x
(2)
解:如图1,连接OB、OD,
y=﹣ ![]() (x﹣4)2+3,则B(4,3)
(x﹣4)2+3,则B(4,3)
平移后的抛物线的对称轴为直线x=4,
当x=4时,y=﹣ ![]() x2=﹣3,则D(4,﹣3),
x2=﹣3,则D(4,﹣3),
∴点B与点D关于x轴对称,
∴阴影部分的面积 S阴影=S△OBD= ![]() ×3×(4+4)=12
×3×(4+4)=12
(3)
解:设直线AB的解析式为y=kx+b,
把A(8,0),B(4,3)代入得 ![]() ,解得
,解得  ,
,
∴直线AB的解析式为y=﹣ ![]() x+6,
x+6,
作NQ⊥x轴于Q,如图2,P(0,6),AP=10,
∵∠PMN为直角,
∴∠PMO+∠QMN=90°,
而∠PMO+∠MOP=90°,
∴∠QMN=∠MOP,
∴△MPO∽△NMQ,
∴ ![]() =
= ![]() ,
,
当NM=NA时,MQ=AQ= ![]() (8﹣t),
(8﹣t),
∴OQ=8﹣ ![]() (8﹣t)=
(8﹣t)= ![]() t+4,
t+4,
当x= ![]() t+4时,y=﹣
t+4时,y=﹣ ![]() (
( ![]() t+4)+6=﹣
t+4)+6=﹣ ![]() t+3;
t+3;
∴ ![]() =
= ![]() ,解得t1=8(舍去),t2=
,解得t1=8(舍去),t2= ![]() ;
;
当AM=AN时,AN=AM=8﹣t,
∵NQ∥OP,
∴△ANQ∽△APO,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
∴NQ= ![]() (8﹣t),AQ=
(8﹣t),AQ= ![]() (8﹣t),
(8﹣t),
∴MQ=8﹣t﹣ ![]() (8﹣t)=
(8﹣t)= ![]() ,
,
∴ ![]() =
= ![]() ,解得t1=8(舍去),t2=18(舍去;
,解得t1=8(舍去),t2=18(舍去;
当MA=MN时,
∵∠OAP<45°,
∴∠MNA=∠NAM<45°,
∴∠AMN>90°,显然不成立,
综上所述,当t为 ![]() 时,△MAN为等腰三角形
时,△MAN为等腰三角形

【解析】(1)利用交点式写出平移后的抛物线解析式;(2)如图1,连接OB、OD,先通过配方法可得到B(4,3),再确定D(4,﹣3),利用对称性可得到阴影部分的面积 S阴影=S△OBD , 然后根据三角形面积公式求解;(3)先利用待定系数法求出直线AB的解析式为y=﹣ ![]() x+6,作NQ⊥x轴于Q,如图2,易得P(0,6),AP=10,再证明△MPO∽△NMQ得到
x+6,作NQ⊥x轴于Q,如图2,易得P(0,6),AP=10,再证明△MPO∽△NMQ得到 ![]() =
= ![]() ,然后讨论:当NM=NA时,MQ=AQ=
,然后讨论:当NM=NA时,MQ=AQ= ![]() (8﹣t),则OQ=
(8﹣t),则OQ= ![]() t+4,接着利用一次函数图象上点的坐标表示出NQ=﹣
t+4,接着利用一次函数图象上点的坐标表示出NQ=﹣ ![]() t+3,则利用相似比得到
t+3,则利用相似比得到 ![]() =
= ![]() ,解方程求出满足条件的t的值;当AM=AN时,AN=AM=8﹣t,证明△ANQ∽△APO,利用相似比可得到NQ=
,解方程求出满足条件的t的值;当AM=AN时,AN=AM=8﹣t,证明△ANQ∽△APO,利用相似比可得到NQ= ![]() (8﹣t),AQ=
(8﹣t),AQ= ![]() (8﹣t),则MQ=8﹣t﹣
(8﹣t),则MQ=8﹣t﹣ ![]() (8﹣t)=
(8﹣t)= ![]() ,然后利用相似比得到
,然后利用相似比得到 ![]() =
= ![]() ,解方程确定满足条件的t的值;当MA=MN时,由于∠OAP<45°,则∠MNA=∠NAM<45°,原式可判断∠AMN>90°,显然不成立,所以当t为
,解方程确定满足条件的t的值;当MA=MN时,由于∠OAP<45°,则∠MNA=∠NAM<45°,原式可判断∠AMN>90°,显然不成立,所以当t为 ![]() 时,△MAN为等腰三角形.
时,△MAN为等腰三角形.









