题目内容
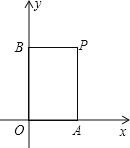
【题目】如图,在正方形ABCD中,△PBC、△QCD是两个等边三角形,PB与DQ交于M,BP与CQ交于E,CP与DQ交于F。
求证:PM=QM。

【答案】证明见解析。
【解析】
试题分析:要证明PM=QM,可以证明△PMF≌△QME,观察图形,容易发现∠P=∠Q=60°,∠PMF=∠QME,关键是找出一组边相等,再联系已知条件,发现由ASA可以证明△EBC≌△FDC,得出CE=CF,从而PF=QE。
试题解析:在正方形ABCD中,△PBC、△QCD都是等边三角形
∴∠QCB=∠PCD=30°(2分)
又∵BC=CD,∠PBC=∠QDC
∴△EBC≌△FDC(4分)
∴CE=CF
又∵CQ=CD=BC=CP
∴PF=QE(5分)
又∵∠P=∠Q,∠QME=∠PMF
∴△MEQ≌△MFP
∴PM=QM(7分)

练习册系列答案
相关题目