题目内容
把两个全等的等腰直角三角板ABC和EFG(其中直角边长约为4)叠放在一起(图1),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O按顺时针方向旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(图2).
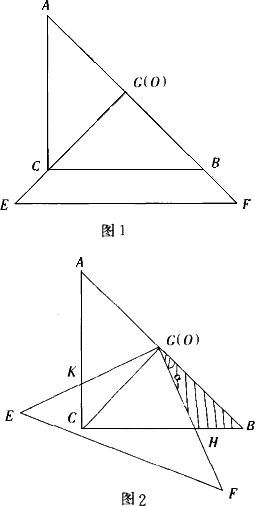
(1)在上述过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论;
(2)连结HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的![]() ?若存在,求出此时x的值,若不存在,说明理由.
?若存在,求出此时x的值,若不存在,说明理由.
答案:
解析:
解析:
|
(1)相等;无变化,都等于△ABC面积的一半.证△GCK≌△GBH. (2)BH=CK=x,CH=4-x,由S△GKH=S四边形CHGK―S△KCH= (3)存在.x=1或x=3. |

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).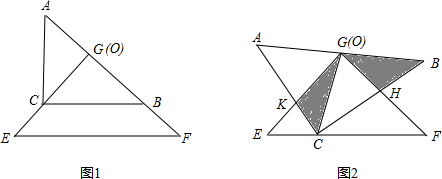
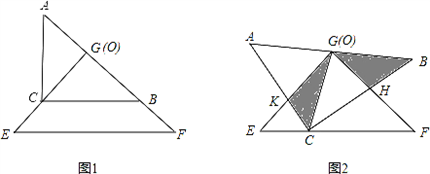
 ?若存在,求出此时x的值;若不存在,说明理由.
?若存在,求出此时x的值;若不存在,说明理由.
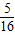 ?若存在,求出此时x的值;若不存在,说明理由.
?若存在,求出此时x的值;若不存在,说明理由.