题目内容
把两个全等的等腰直角三角板△ABC和△EFG（其直角边长均为4）叠放在一起（如图1），且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合．现将三角板EFG绕O点顺时针方向旋转（旋转角满足条件：0°＜α＜90°），四边形CHGK是旋转过程中两三角板的重叠部分（如图2）．在上述旋转过程中，BH与CK有怎样的数量关系？四边形CHGK的面积有何变化？证明你发现的结论．
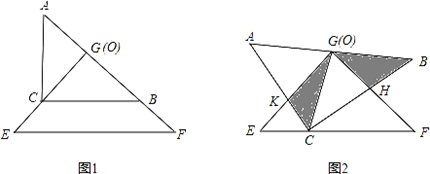
解：在上述旋转过程中，BH=CK，四边形CHGK的面积不变．
证明：连接CG，
∵△ABC为等腰直角三角形，G（O）为其斜边中点，
∴CG=BG，CG⊥AB，且S△BCG=
S△ABC．
∴∠ACG=∠B=45°．
∵∠BGH与∠CGK均为旋转角，
∴∠BGH=∠CGK．
∴△BGH≌△CGK．
∴BH=CK，
S△BGH=S△CGK．
∴S四边形CHGK=S△CHG+S△CGK=S△CHG+S△BGH=S△BCG=
S△ABC=
×
×4×4=4．
即：旋转过程中，BH=CK，S四边形CHGK的面积为4，是一个定值，在旋转过程中没有变化．
证明：连接CG，
∵△ABC为等腰直角三角形，G（O）为其斜边中点，
∴CG=BG，CG⊥AB，且S△BCG=
S△ABC．∴∠ACG=∠B=45°．
∵∠BGH与∠CGK均为旋转角，
∴∠BGH=∠CGK．
∴△BGH≌△CGK．
∴BH=CK，
S△BGH=S△CGK．
∴S四边形CHGK=S△CHG+S△CGK=S△CHG+S△BGH=S△BCG=
S△ABC=××4×4=4．即：旋转过程中，BH=CK，S四边形CHGK的面积为4，是一个定值，在旋转过程中没有变化．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
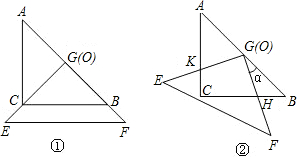把两个全等的等腰直角三角形ABC和EFG（其直角边长均为4）叠放在一起（如图①），且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合．现将三角板EFG绕O点逆时针旋转（旋转角α满足条件：0°＜α＜90°），四边形CHGK是旋转过程中两三角板的重叠部分（如图②）．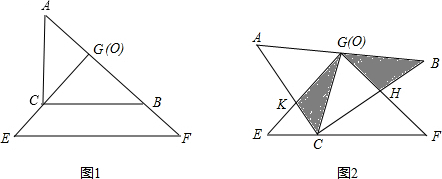
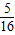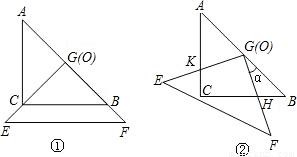
？若存在，求出此时x的值；若不存在，说明理由．
？若存在，求出此时x的值；若不存在，说明理由．