题目内容
把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).(1)在上述旋转过程中,BH与CK有怎样的数量关系四边形CHGK的面积有何变化?证明你发现的结论;
(2)连接HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的
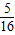 ?若存在,求出此时x的值;若不存在,说明理由.
?若存在,求出此时x的值;若不存在,说明理由.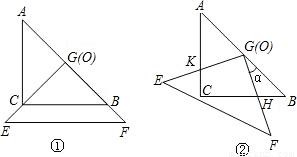
【答案】分析:(1)可将四边形CHGK分成两部分,然后通过证三角形全等,将四边形的面积进行转换来求解.连接CG,可通过证明三角形CGK与三角形BGH全等来得出他们的面积相等,进而将四边形CHGK的面积转换成三角形CGB的面积也就是三角形ABC面积的一半,由此可得出四边形CHGK的面积是4,所以不会改变;
(2)连接HK后,根据(1)中得出的四边形CHGK的面积为4,可根据三角形GHK的面积=四边形CHGK的面积-三角形CHK的面积来求,如果BH=x,那么根据(1)的结果CK=x,有BC的长,那么CH=4-x,由此可得出关于x,y的函数关系式.x的取值范围应该大于零小于4;
(3)只需将y=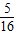 ×8代入(2)的函数式中,可得出x的值.然后判断x是否符合要求即可.
×8代入(2)的函数式中,可得出x的值.然后判断x是否符合要求即可.
解答:解:(1)在上述旋转过程中,BH=CK,四边形CHGK的面积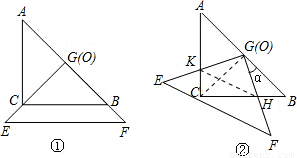 不变.
不变.
证明:连接CG,KH,
∵△ABC为等腰直角三角形,O(G)为其斜边中点,
∴CG=BG,CG⊥AB,
∴∠ACG=∠B=45°,
∵∠BGH与∠CGK均为旋转角,
∴∠BGH=∠CGK,
在△BGH与△CGK中,

∴△BGH≌△CGK(ASA),
∴BH=CK,S△BGH=S△CGK.
∴S四边形CHGK=S△CHG+S△CGK=S△CHG+S△BGH= S△ABC=
S△ABC= ×
× ×4×4=4,
×4×4=4,
即:S四边形CHGK的面积为4,是一个定值,在旋转过程中没有变化;
(2)∵AC=BC=4,BH=x,
∴CH=4-x,CK=x.
由S△GHK=S四边形CHGK-S△CHK,
得y=4- x(4-x),
x(4-x),
∴y= x2-2x+4.
x2-2x+4.
由0°<α<90°,得到BH最大=BC=4,
∴0<x<4;
(3)存在.
根据题意,得 x2-2x+4=
x2-2x+4=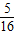 ×8,
×8,
解这个方程,得x1=1,x2=3,
即:当x=1或x=3时,△GHK的面积均等于△ABC的面积的 .
.
点评:本题主要考查了等腰直角三角形的性质以及全等三角形的判定等知识点,通过构建全等三角形将面积进行转换是解题的关键.
(2)连接HK后,根据(1)中得出的四边形CHGK的面积为4,可根据三角形GHK的面积=四边形CHGK的面积-三角形CHK的面积来求,如果BH=x,那么根据(1)的结果CK=x,有BC的长,那么CH=4-x,由此可得出关于x,y的函数关系式.x的取值范围应该大于零小于4;
(3)只需将y=
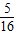 ×8代入(2)的函数式中,可得出x的值.然后判断x是否符合要求即可.
×8代入(2)的函数式中,可得出x的值.然后判断x是否符合要求即可.解答:解:(1)在上述旋转过程中,BH=CK,四边形CHGK的面积
 不变.
不变.证明:连接CG,KH,
∵△ABC为等腰直角三角形,O(G)为其斜边中点,
∴CG=BG,CG⊥AB,
∴∠ACG=∠B=45°,
∵∠BGH与∠CGK均为旋转角,
∴∠BGH=∠CGK,
在△BGH与△CGK中,

∴△BGH≌△CGK(ASA),
∴BH=CK,S△BGH=S△CGK.
∴S四边形CHGK=S△CHG+S△CGK=S△CHG+S△BGH=
 S△ABC=
S△ABC= ×
× ×4×4=4,
×4×4=4,即:S四边形CHGK的面积为4,是一个定值,在旋转过程中没有变化;
(2)∵AC=BC=4,BH=x,
∴CH=4-x,CK=x.
由S△GHK=S四边形CHGK-S△CHK,
得y=4-
 x(4-x),
x(4-x),∴y=
 x2-2x+4.
x2-2x+4.由0°<α<90°,得到BH最大=BC=4,
∴0<x<4;
(3)存在.
根据题意,得
 x2-2x+4=
x2-2x+4=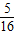 ×8,
×8,解这个方程,得x1=1,x2=3,
即:当x=1或x=3时,△GHK的面积均等于△ABC的面积的
 .
.点评:本题主要考查了等腰直角三角形的性质以及全等三角形的判定等知识点,通过构建全等三角形将面积进行转换是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
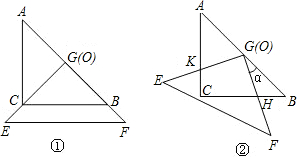 把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).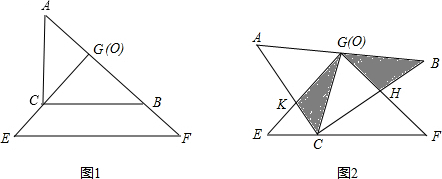
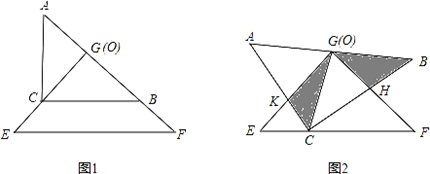
 ?若存在,求出此时x的值;若不存在,说明理由.
?若存在,求出此时x的值;若不存在,说明理由.