题目内容
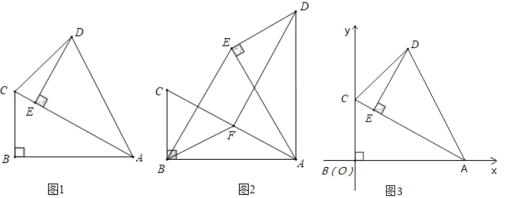
【题目】如图，点
为
的
边的中点，分别以
、
为斜边作
和
，且
，
．
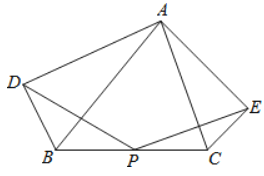
（1）求证：
．
（2）探究：
与
的数量关系，并证明你的结论．
【答案】（1）详见解析；（2）
，证明见解析．
【解析】
（1）如图，分别取
、
的中点
、
，连接
、
、
、
，根据三角形的中位线定理和直角三角形的性质可得
，
，根据等腰三角形的性质、三角形的外角性质和已知条件可得
，根据平行线的性质可得
=
，进而可得
，于是可根据SAS证明
，从而可得结论；
（2）根据平行线的性质可得
，根据全等三角形的性质可得
，然后在
中利用三角形的内角和定理和等量代换即可得出结论．
（1）证明：如图，分别取、的中点、，连接、、、．
点
为
的边
的中点，
∴
，
为
斜边上的中线，
∴
，
，
同理可得：，
，
，
，
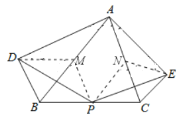
同理，
，
又
，
，
又、都是的中位线，
，
，
，
，
，
∴，
，
；
（2）解：
与
的数量关系是：；
证明：
，
，
∵，
，
在中，∵
，
∴
，
而
，
，
，
．
练习册系列答案
相关题目
【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，把超过或不足的部分分别用正、负数来表示，记录如下表：
与标准质量的差值（单位：克） | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
（1）若每袋食品的标准质量为450克，则抽样检测的20袋食品的总质量是多少克？
（2）若该种食品的合格标准为450±5克，求该种食品抽样检测的合格率？
