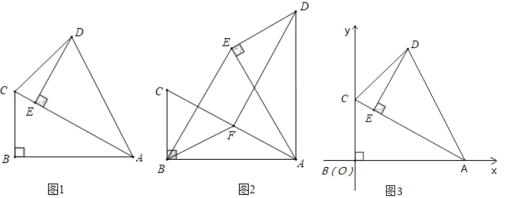
题目内容
【题目】在![]() 中,∠ABC=90°,∠BAC=30°,将
中,∠ABC=90°,∠BAC=30°,将![]() 绕点A顺时针旋转一定的角度α得到
绕点A顺时针旋转一定的角度α得到![]() ,点B、C的对应点分别是E、D.
,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若α=60°时,点F是边AC中点,求证:DF=BE;
(3)如图3,点B、C的坐标分别是(0,0),(0,2),点Q是线段AC上的一个动点,点M是线段AO上的一个动点,是否存在这样的点Q、M使得![]() 为等腰三角形且
为等腰三角形且![]() 为直角三角形?若存在,请直接写出满足条件的点M的坐标;若不存在,请说明理由.
为直角三角形?若存在,请直接写出满足条件的点M的坐标;若不存在,请说明理由.
【答案】(1)15°;(2)证明见解析;(3)M(![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
(1)由旋转的性质得出![]() ,
,![]() ,利用等腰三角形的性质求出
,利用等腰三角形的性质求出![]() ,进而得解;
,进而得解;
(2)通过证明![]() 与
与![]() 是等边三角形,
是等边三角形,![]() ,进而得证;
,进而得证;
(3)分两种情况考虑:①当![]() 时,要使得△CQM为等腰三角形,则
时,要使得△CQM为等腰三角形,则![]() ,②当
,②当![]() 时,要使得△CQM为等腰三角形,则
时,要使得△CQM为等腰三角形,则![]() ,分别求解即可.
,分别求解即可.
解:(1)∵∠ABC=90°,∠BAC=30°,
∵将![]() 绕点A顺时针旋转一定的角度α得到
绕点A顺时针旋转一定的角度α得到![]() ,且点E恰好在AC上,
,且点E恰好在AC上,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)由题意知,![]() ,
,![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵点F是![]() 的边AC的中点,
的边AC的中点,
∴![]() ,
,
∵∠BAC=30°,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
在![]() 与
与![]() 中,
中,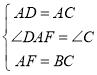 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)分两种情况考虑:
∵![]() ,
,![]() ,
,
∴![]() ,由勾股定理知,
,由勾股定理知,![]() ,
,
设点![]() ,
,
①当![]() 时,要使得△CQM为等腰三角形,则
时,要使得△CQM为等腰三角形,则![]() ,
,
∴![]() ,
,![]() ,
,
∴由勾股定理知,![]() ,即
,即![]() ,
,
解得,![]() (负值舍去),
(负值舍去),![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得,![]() ,
,
∴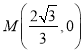 ;
;
②当![]() 时,要使得△CQM为等腰三角形,则
时,要使得△CQM为等腰三角形,则![]() ,
,
∴![]() ,由勾股定理知,
,由勾股定理知,![]() ,
,![]() ,
,
∴![]() ,
,
解得,![]() ,
,
∴![]() ,
,
综上所述,存在,点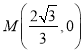 或
或![]() .
.

【题目】某学校计划租用6辆客车送一批师生参加一年一度的哈尔滨冰雕节,感受冰雕艺术的魅力.现有甲、乙两种客车,它们的载客量和租金如下表.设租用甲种客车x辆,租车总费用为y元.
甲种客车 | 乙种客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 280 | 200 |
(1)求出y(元)与x(辆)之间的函数关系式,指出自变量的取值范围;
(2)若该校共有240名师生前往参加,领队老师从学校预支租车费用1650元,试问预支的租车费用是否可以结余?若有结余,最多可结余多少元?