题目内容
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,AD是∠BAC的平分线.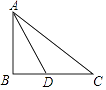
(1)尺规作图:过点D作DE⊥AC于E;
(2)求DE的长.
【答案】
(1)
解:方法1,如图1所示,过点D作AC的垂线即可;
方法2:运用角平分线的性质,以点D为圆心,BD的长为半径画圆,⊙D和AC相切于点E,连接DE即可.

(2)
解:方法一:设DE=x,则AC= ![]() =5.
=5.
∵AD是∠BAC的平分线,∠ABC=90°,DE⊥AC,
∴BD=DE=x,CD=BC﹣BD=4﹣x.
∵S△ACD= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,解得x=
,解得x= ![]() ,
,
∴DE=x= ![]() .
.
方法二:设DE=x,则AC= ![]() =5.
=5.
∵AD是∠BAC的平分线,∠ABC=90°,DE⊥AC,
∴BD=DE=x,CD=BC﹣BD=4﹣x.
∵∠DEC=∠ABC=90°,∠C=∠C,
∴△DEC∽△ABC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,解得x=
,解得x= ![]() ,
,
∴DE=x= ![]() .
.
方法三:设DE=x,则AC= ![]() =5.
=5.
∵AD是∠BAC的平分线,∠ABC=90°,DE⊥AC,
∴BD=DE=x,CD=BC﹣BD=4﹣x.
∵在Rt△ABC中,sin∠C= ![]() =
= ![]() ,
,
在Rt△DEC中,sin∠C= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,解得x=
,解得x= ![]() ,
,
∴DE=x= ![]() .
.
【解析】(1)根据过直线外一点作直线垂线的作法即可画出图形;(2)设DE=x,则AC= ![]() =5,跟进吧AD是∠BAC的平分线,∠ABC=90°,DE⊥AC可得出BD=DE=x,CD=BC﹣BD=4﹣x,再由S△ACD=
=5,跟进吧AD是∠BAC的平分线,∠ABC=90°,DE⊥AC可得出BD=DE=x,CD=BC﹣BD=4﹣x,再由S△ACD= ![]() =
= ![]() 求出x的值即可.
求出x的值即可.
【考点精析】利用角平分线的性质定理对题目进行判断即可得到答案,需要熟知定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.