题目内容
如图，在Rt△ABC中，∠ACB=90°，D在AB上，四边形DECF是正方形，若BD=3cm，AD=2cm,则图中阴影部分面积为________________________.
3
过D点作DG⊥AB交AC于G．通过证明△DFG≌△DEA，得出DG=DA=2cm，从而求得S△BDG，即阴影部分面积的和．
解：过D点作DG⊥AB交AC于G．
∵∠EDG+∠EDA=∠EDG+∠GDF，
∴∠GDF=∠EDA．
∵DE=DF，∠DFG=∠DEA，
∴△DFG≌△DEA．
∴DG=DA=2cm．
∴阴影部分面积的和=S△BDG=
=3cm2．
故答案为：3cm2．
解：过D点作DG⊥AB交AC于G．
∵∠EDG+∠EDA=∠EDG+∠GDF，
∴∠GDF=∠EDA．
∵DE=DF，∠DFG=∠DEA，
∴△DFG≌△DEA．
∴DG=DA=2cm．
∴阴影部分面积的和=S△BDG=
=3cm2．故答案为：3cm2．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
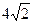cm，∠C=45°，点P从B点出发，沿着BC方向以1cm/s运动，到达点C停止，设P运动了ts。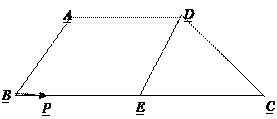
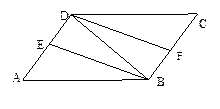
A1BCD1,若
