题目内容
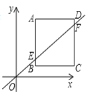
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点,过点
是抛物线的顶点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.
(1)求此抛物线的解析式;
(2)点![]() 是抛物线上的动点,设点
是抛物线上的动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②过点![]() 作
作![]() 轴,与抛物线交于点
轴,与抛物线交于点![]() ,
,![]() 为
为![]() 轴上一点,连接
轴上一点,连接![]() ,
,![]() ,将
,将![]() 沿着
沿着![]() 翻折,得
翻折,得![]() ,若四边形
,若四边形![]() 恰好为正方形,直接写出
恰好为正方形,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)①点
;(2)①点![]() 坐标为
坐标为![]() 或
或![]() ;②
;②![]() 或
或![]()
【解析】
(1)利用待定系数法即可解决问题;
(2)①根据![]() ,
,![]() ,由
,由![]() ,构建方程即可解决问题;②因为点M、N关于抛物线的对称轴对称,四边形MPNQ是正方形,推出点P是抛物线的对称轴与x轴的交点,即
,构建方程即可解决问题;②因为点M、N关于抛物线的对称轴对称,四边形MPNQ是正方形,推出点P是抛物线的对称轴与x轴的交点,即![]() ,易证
,易证![]() ,即
,即![]() ,解方程即可解决问题.
,解方程即可解决问题.
解:(1)∵![]() ,
,![]() 在
在![]() 上
上
∴![]()
解得![]()
∴![]()
(2)①∵点![]() 为抛物线的顶点,
为抛物线的顶点,![]() 轴
轴
∴![]() ,
,![]() ,
,![]()
∴![]()
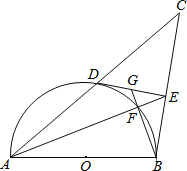
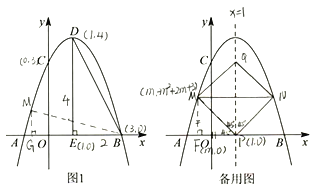
如图1过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,则
,则![]() .
.
∵![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
∵![]() ∴
∴![]()
解得![]() ,
,![]() (舍),
(舍),![]() ,
,![]() (舍)
(舍)
综上,满足条件的点![]() 坐标为
坐标为![]() 或
或![]()
②![]() 的值为
的值为![]() 或
或![]() 或
或![]() 或
或![]()
![]() 为正方形,
为正方形,![]() 轴,
轴,![]() ,
,![]() 关于对称轴对称
关于对称轴对称
∴![]() 为等腰
为等腰![]() ,
,![]()
∴![]() 为等腰
为等腰![]() ,
,![]()
∴![]()
![]() 或
或![]()

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目