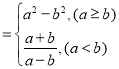题目内容
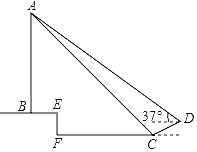
【题目】如果三角形的两个内角∠α与∠β满足2α+β=90°,那么,我们将这样的三角形称为“准互余三角形”.在△ABC中,已知∠C=90°,BC=3,AC=4(如图所示),点D在AC边上,联结BD.如果△ABD为“准互余三角形”,那么线段AD的长为_____(写出一个答案即可).

【答案】![]() 或
或![]()
【解析】
作DM⊥AB于M.设∠ABD=α,∠A=β.分两种情形:①当2α+β=90°时.②当α+2β=90°时,分别求解即可.
解:过点D作DM⊥AB于M.设∠ABD=α,∠A=β.
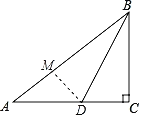
①当2α+β=90°时,∵α+β+∠DBC=90°,
∴∠DBC=∠DBA,
∵DM⊥AB,DC⊥BC,
∴DM=DC,
∵∠DMB=∠C=90°,DM=DC,BD=BD,
∴Rt△BDC≌Rt△BDM(HL),
∴BM=BC=3,
∵∠C=90°,BC=3,AC=4,
∴AB=![]() =5,
=5,
∴AM=5﹣3=2,设AD=x,则CD=DM=4﹣x,
在Rt△ADM中,则有x2=(4﹣x)2+22,
解得x=![]() .
.
∴AD=![]() .
.
②当α+2β=90°时,∵α+β+∠DBC=90°,
∴∠DBC=β=∠A,
∵∠C=∠C,
∴△CBD∽△CAB,
∴BC2=CDCA,
∴CD=![]() ,
,
∴AD=AC﹣CD=4﹣![]() =
=![]() .
.
故答案为:![]() 或
或![]() .
.

【题目】红旗连锁超市准备购进甲、乙两种绿色袋装食品.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于4800元,且不超过4900元,问该超市有几种进货方案?
(3)在(2)的条件下,该超市如果对甲种袋裝食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
【题目】为响应市政府关于“垃圾不落地,市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的了解情况,对该校部分学生进行了问卷调查,并将调查结果分为![]() 四类(其中
四类(其中![]() 类表示“非常了解”,
类表示“非常了解”,![]() 类表示“比较了解”,
类表示“比较了解”,![]() 类表示“基本了解”,
类表示“基本了解”,![]() 类表示“不太了解”).根据调查结果得到如下不完整的统计表和统计图.请解答下列问题:
类表示“不太了解”).根据调查结果得到如下不完整的统计表和统计图.请解答下列问题:
了解程度 | 人数(人) | 所占百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
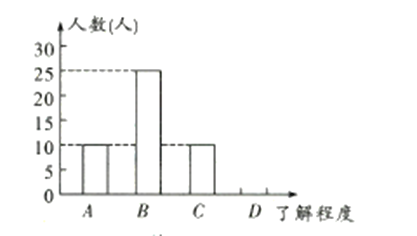
![]() ,
,![]() .
.
![]() 补全条形统计图;
补全条形统计图;
![]() 若该校共有学生
若该校共有学生![]() 人,估计该校对垃圾分类知识“非常了解”的有多少人?
人,估计该校对垃圾分类知识“非常了解”的有多少人?