题目内容
对抛物线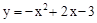 而言,下列结论正确的是
而言,下列结论正确的是
A.与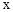 轴有两个交点 轴有两个交点 | B.开口向上 |
C.与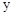 轴交点坐标是(0,3) 轴交点坐标是(0,3) | D.顶点坐标是(1,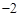 ) ) |
D.
解析试题分析:根据二次函数的图象与系数的关系、顶点坐标及二次函数图象上点的坐标特点对各小题进行逐一分析即可:
A.由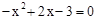 的
的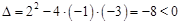 知
知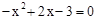 无实根,故抛物线
无实根,故抛物线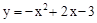 与
与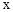 轴没有交点;
轴没有交点;
B.由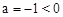 知抛物线
知抛物线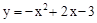 开口向下;
开口向下;
C.由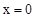 时,
时,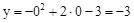 知抛物线
知抛物线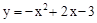 与
与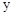 轴交点坐标是(0,
轴交点坐标是(0,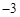 ) ;
) ;
D.由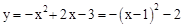 知抛物线
知抛物线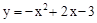 顶点坐标是(1,
顶点坐标是(1,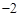 ).
).
故选D.
考点:二次函数的性质.

练习册系列答案
相关题目
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④3a+c=0;则其中说法正确的是( ).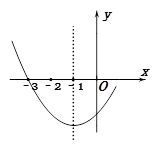
| A.①② | B.②③ | C.①②④ | D.②③④ |
抛物线y=x2-2mx+m2+m+1的顶点在( )
| A.直线y=x上 | B.直线y=x-1上 |
| C.直线x+y+1=0上 | D.直线y=x+1上 |
把二次函数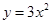 的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系式是( )
的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系式是( )
A.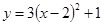 | B.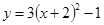 ; ; |
C.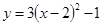 | D. |
把抛物线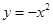 向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A.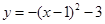 | B. |
C.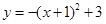 | D.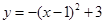 |
已知二次函数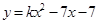 的图象与x轴没有交点,则k的取值范围为
的图象与x轴没有交点,则k的取值范围为
A.k﹥-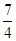 | B.k≥-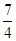 且k≠0 且k≠0 |
C.k﹤-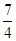 | D.k﹥-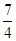 且k≠0 且k≠0 |
在平面直角坐标系中,将函数y=2x2的图象先向右平移1个单位,再向上平移5个单位得到图象的函数关系式是( )
| A.y=2(x-1)2-5 | B.y=2(x-1)2+5 |
| C.y=2(x+1)2-5 | D.y=2(x+1)2+5 |
将抛物线y=(x﹣1)2+3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为( )
| A.y=(x﹣2)2 | B.y=(x﹣2)2+6 | C.y=x2+6 | D.y=x2 |