题目内容
如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )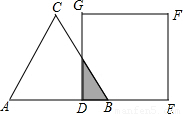
A.
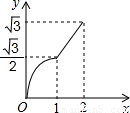
B.
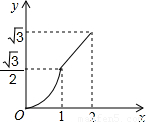
C.
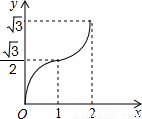
D.
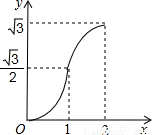
【答案】分析:此题可分为两段求解,即B从D点运动到DE的中点和A从DE的中点运动到E点,列出面积随动点变化的函数关系式即可.
解答:解:设BD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,
当B从D点运动到DE的中点时,即0≤x≤1时,y= ×x×
×x×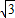 x=
x= x2.
x2.
当B从DE中点运动到E点时,即1<x≤2时,y= -
- (2-x)×
(2-x)×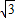 (2-x)=-
(2-x)=- x2+2
x2+2 x-
x-
由函数关系式可看出D中的函数图象与所求的分段函数对应.
故选D.
点评:本题考查的动点变化过程中面积的变化关系,重点是列出函数关系式,但需注意自变量的取值范围.
解答:解:设BD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,
当B从D点运动到DE的中点时,即0≤x≤1时,y=
 ×x×
×x×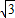 x=
x= x2.
x2.当B从DE中点运动到E点时,即1<x≤2时,y=
 -
- (2-x)×
(2-x)×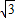 (2-x)=-
(2-x)=- x2+2
x2+2 x-
x-
由函数关系式可看出D中的函数图象与所求的分段函数对应.
故选D.
点评:本题考查的动点变化过程中面积的变化关系,重点是列出函数关系式,但需注意自变量的取值范围.

练习册系列答案
相关题目
 如图,等边△ABC的边长为l,取边AC的中点D,在外部画出一个新的等边三角形△CDE,如此绕点C顺时针继续下去,直到所画等边三角形的一边与△ABC的BC边重叠为止,此时这个三角形的边长为
如图,等边△ABC的边长为l,取边AC的中点D,在外部画出一个新的等边三角形△CDE,如此绕点C顺时针继续下去,直到所画等边三角形的一边与△ABC的BC边重叠为止,此时这个三角形的边长为 10、如图,等边△ABC的三条角平分线相交于点O,OD∥AB交BC于D,OE∥AC交BC于点E,那么这个图形中的等腰三角形共有( )
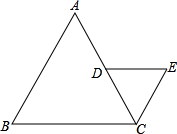
10、如图,等边△ABC的三条角平分线相交于点O,OD∥AB交BC于D,OE∥AC交BC于点E,那么这个图形中的等腰三角形共有( )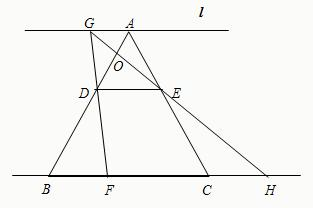 已知:如图,等边△ABC的边长为6,点D、E分别在AB、AC上,且AD=AE=2,直线l过点A,且l∥BC,若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设F点运动的时间为t秒,当t>0时,直线DF交l于点G,GE的延长线与BC的延长线交于点H,AB与GH相交于点O.
已知:如图,等边△ABC的边长为6,点D、E分别在AB、AC上,且AD=AE=2,直线l过点A,且l∥BC,若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设F点运动的时间为t秒,当t>0时,直线DF交l于点G,GE的延长线与BC的延长线交于点H,AB与GH相交于点O.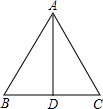 如图,等边△ABC的边长为2,AD是△ABC的角平分线,
如图,等边△ABC的边长为2,AD是△ABC的角平分线,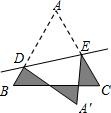 如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为( )
如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为( )