Question

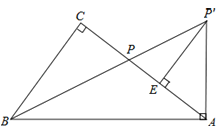
【题目】如图，在Rt△ABC中，∠C=90°，点P为AC边上的一点，将线段AP绕点A顺时针方向旋转（点P对应点P′），当AP旋转至AP′⊥AB时，点B、P、P′恰好在同一直线上，此时作P′E⊥AC于点E．

（1）求证：∠CBP=∠ABP；

（2）求证：AE=CP；

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）根据旋转的性质可得,根据等边对等角的性质可得,再根据等角的余角相等证明即可;

（2）过P点作PD⊥AB于点D，根据角平分线上的点到角的两边的距离相等可得,然后求出,利用"角角边",根据全等三角形对应边相等可得,从而得证.

证明：（1）∵是由旋转得到，

∴，

∴，

∵∠C=90°，AP′⊥AB

∴，

又∵

∴

（2）如图，过P点作PD⊥AB于点D，

∵

∴，

∵

∴

∴

在和中，

∴

∴

∴