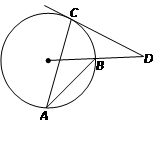题目内容
如图,从⊙O外一点A引圆的切线AB,切点为B,连接AO 并延长交圆于点C,连接BC.若∠A=26°,则∠ACB的度数为 ▲ .



连接OB,根据切线的性质,得∠OBA=90°,又∠A=26°,所以∠AOB=64°,再用三角形的外角性质可以求出∠ACB的度数.
解答: 解:如图:连接OB,
解:如图:连接OB,
∵AB切⊙O于点B,
∴∠OBA=90°,
∵∠A=26°,
∴∠AOB=90°-26°=64°,
∵OB=OC,
∴∠C=∠OBC,
∵∠AOB=∠C+∠OBC=2∠ACB,
∴∠ACB=32°.
解答:
 解:如图:连接OB,
解:如图:连接OB,∵AB切⊙O于点B,
∴∠OBA=90°,
∵∠A=26°,
∴∠AOB=90°-26°=64°,
∵OB=OC,
∴∠C=∠OBC,
∵∠AOB=∠C+∠OBC=2∠ACB,
∴∠ACB=32°.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目

 交x轴于A、B两点,顶点为C,经过A、B、C三点的圆的圆心为M.
交x轴于A、B两点,顶点为C,经过A、B、C三点的圆的圆心为M.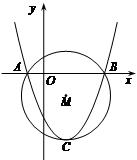 点D的坐标,若不存在,请说明理由.
点D的坐标,若不存在,请说明理由. 是
是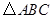 的外接圆,
的外接圆,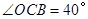 ,则
,则 的度数等于___________.
的度数等于___________.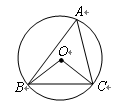
 是
是 的直径,弦
的直径,弦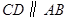 .若
.若 ,则
,则 .
.