题目内容
【题目】如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,求AB两点的距离.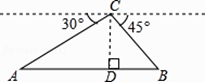
【答案】解:∵从热气球C处测得地面A、B两点的俯角分别为30°、45°,
∴∠BCD=90°﹣45°=45°,∠ACD=90°﹣30°=60°,
∵CD⊥AB,CD=100米,
∴△BCD是等腰直角三角形,
∴BD=CD=100米,
在Rt△ACD中,
∵CD=100米,∠ACD=60°,
∴AD=CDtan60°=100× ![]() =100
=100 ![]() (米),
(米),
∴AB=AD+BD=100 ![]() +100=100(
+100=100( ![]() +1)米.
+1)米.
答:AB两点的距离是100( ![]() +1)米.
+1)米.
【解析】
【考点精析】通过灵活运用关于仰角俯角问题,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目