题目内容
某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,若这种商品每件的销售价每提高0.5元,其销售量就减少10件.问(1)每件售价定为多少元时,才能使利润为640元?(2)每件售价定为多少元时,才能使利润最大?
(1)12或16元;(2)14.
解析试题分析:(1)根据等量关系“利润=(售价-进价)×销量”列出函数关系式;(2)根据(1)中的函数关系式求得利润最大值.
试题解析:(1)设每件售价定为x元时,才能使每天利润为640元,
则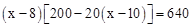 ,解得:x1=12,x2=16.
,解得:x1=12,x2=16.
答:应将每件售价定为12或16元时,能使每天利润为640元.
(2)设利润为y:
则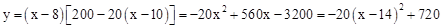 ,
,
∴当售价定为14元时,获得最大利润;最大利润为720元.
考点:二次函数和一元二次方程的应用.

练习册系列答案
相关题目
 .
.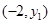 与
与 在此二次函数的图象上,则
在此二次函数的图象上,则
 (填 “>”、“=”或“<”);
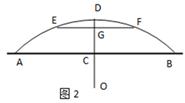
(填 “>”、“=”或“<”); ,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
 与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,
与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C, ,且S△AOC=1,过点P作PB⊥y轴于点B.
,且S△AOC=1,过点P作PB⊥y轴于点B.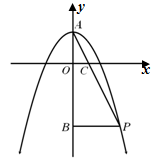
 过两点(m,0)、(n,0),且
过两点(m,0)、(n,0),且 ,抛物线于双曲线
,抛物线于双曲线 (x>0)的交点为(1,d).
(x>0)的交点为(1,d). 都在双曲线
都在双曲线 ,O为坐标原点,记
,O为坐标原点,记 ,点Q在双曲线
,点Q在双曲线 。
。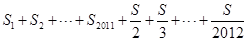 的值.
的值. 的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).


 两种产品,根据市场调研,发现如下信息:
两种产品,根据市场调研,发现如下信息: 种产品所获利润
种产品所获利润 (万元)与所售产品
(万元)与所售产品 (吨)之间存在二次函数关系
(吨)之间存在二次函数关系 .当
.当 时,
时, ;当
;当 时,
时, .
.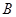 种产品所获利润
种产品所获利润 .
.