题目内容
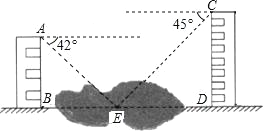
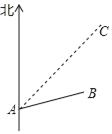
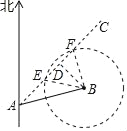
【题目】如图,台风中心位于点A,并沿东北方向AC移动,已知台风移动的速度为50千米/时,受影响区域的半径为130千米,B市位于点A的北偏东75°方向上,距离A点240千米处.
(1)说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
【答案】(1)见解析;(2)2小时.
【解析】
(1)作BD⊥AC于点D,在Rt△ABD中,利用含30°角的直角三角形的性质求出BD的长与130千米相比较即可.
(2)以B为圆心,以130为半径作圆交AC于E,F两点,根据垂径定理即可求出BE=BF=130,然后由勾股定理求得EF的长度,进而求出台风影响B市的时间.
解:(1)如图,作BD⊥AC于点D.
在Rt△ABD中,由条件知,AB=240,∠BAC=75°﹣45°=30°,
∴BD=240×![]() =120<130,
=120<130,
∴本次台风会影响B市.
(2)如图,以点B为圆心,以130为半径作圆交AC于E,F,
若台风中心移动到E时,台风开始影响B市,台风中心移动到F时,台风影响结束.
由(1)得BD=240,由条件得BE=BF=130,
∴EF=![]() =100,
=100,
∴台风影响的时间t=![]() =2(小时).
=2(小时).
故B市受台风影响的时间为2小时.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】利民商场经营某种品牌的T恤,购进时的单价是300元,根据市场调查:在一段时间内,销售单价是400元时,销售量是60件,销售单价每涨10元,销售量就减少1件.设这种T恤的销售单价为x元(x>400)时,销售量为y件、销售利润为W元.
(1)请分别用含x的代数式表示y和W(把结果填入下表):
销售单价(元) | x |
销售量y(件) | |
销售利润W(元) |
(2)该商场计划实现销售利润10000元,并尽可能增加销售量,那么x的值应当是多少?