��Ŀ����
����Ŀ������ģ�ͣ�
��ͼ1������Rt��ABC�У���ABC��90����CB��BA��ֱ��ED������B����A��AD��ED��D����C��CE��ED��E.����֤��ADB����BEC.���ģ�����dz�֮Ϊ��һ������ֱ��.��������б���߶�AB��ֱ�ǡ�ABCת��Ϊ��ƽ��ֱ���߶κ�ֱ�ǣ�������ƽ��ֱ������ϵ�б�����ʹ��.

ģ��Ӧ�ã�
(1)��ͼ2����A��0��4)����B(3��0������ABC�ǵ���ֱ�������Σ�
������ABC��90�����ҵ�C�ڵ�һ���ޣ����C�����ꣻ
����ABΪֱ�DZߣ����C�����ꣻ
(2)��ͼ3��������MFNO��OΪ����ԭ�㣬F������Ϊ��8��6����M��N�ֱ����������ϣ�P���߶�NF�϶��㣬��PN��n����֪��G�ڵ�һ���ޣ�����ֱ��y��2xһ6�ϵ�һ�㣬����MPG����GΪֱ�Ƕ���ĵ���ֱ�������Σ���ֱ��д����G������.
���𰸡���1���٣�7,3�����ڣ�7,3������4,7������-4,1������-1,-3������2����4��2����![]() .
.
��������
��1���ٹ�C��CD��ֱ��x�ṹ����һ������ֱ�����ٸ���ȫ�������ε�������⼴�ɣ��ڵ�C���Ĵ����ֱ�����ͼ�Σ�������һ������ֱ����Գ���⼴�ɣ���2������GΪֱ�Ƕ���ʱ���ֵ�G�ھ���MFNO���ڲ����ⲿ�������������һ������ֱ����⼴�ɣ�
��1������ͼ����C��CD��ֱ��x�ᣬ
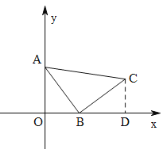
���ݡ�һ������ֱ���ɵá�AOB�ա�BDC����AO=BD��OB=CD��
�ߵ�A��0��4)����B(3��0������AO=4��OB=3 ��
��OD=3+4=7��
���C��������7,3����
����ͼ����ABΪֱ�DZߣ���C��λ�ÿ���4����
a������C�ڢٵ�λ�ô������C������Ϊ��7,3����
b������C��![]() ��λ�ô���ͬ���ɵã����
��λ�ô���ͬ���ɵã����![]() ������Ϊ��4,7����
��������4,7����
c������C��![]() ��λ�ô�����
��λ�ô�����![]() ��
��![]() ���ڵ�A�Գƣ�
���ڵ�A�Գƣ�
�ߵ�A��0��4)����![]() ��4,7�������
��4,7�������![]() ��������-4,1����
��������-4,1����
d������C��![]() ��λ�ô�����
��λ�ô�����![]() ��C���ڵ�B�Գƣ�
��C���ڵ�B�Գƣ�
�ߵ�B(3��0������C��7,3�������![]() ������Ϊ��-1,-3����
��������-1,-3����
���ϣ���C������Ϊ��7,3������4,7������-4,1������-1,-3����
��2������Gλ��ֱ��y=2x-6��ʱ�������������
�ٵ���G�ھ���MFNO���ڲ�ʱ����ͼ����G��x���ƽ����AB����y����A����ֱ��NF�ڵ�B����G��x��2x-6����

��OA=2x-6��AM=6-��2x-6��=12-2x��BG=AB-AG=8-x��
���MAG�ա�GBP����AM =BG��
����12-2x=8-x�����x=4��
��G��4��2����
����G�ھ���MFNO���ⲿʱ����ͼ����G��x���ƽ����AB����y����A����ֱ��NF���ӳ����ڵ�B����G��x��2x-6����
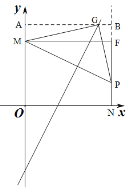
��OA=2x-6��AM=��2x-6��-6=2x-12��BG=AB-AG=8-x��
���MAG�ա�GBP����AM =BG��
����2x-12=8-x�����![]() ��
��
��G ![]() ��
��
���ϣ�G�������Ϊ��4��2����![]() .
.

 �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д� ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�����Ŀ����ǿ��������λͬѧ��ѧϰ��������ʱ����������(��������״)���������ǹ�����54�����������ϵ����Ĵ������±���
���ϵ��� | 1 | 2 | 3 | 4 | 5 | 6 |
���ִ��� | 6 | 9 | 5 | 8 | 16 | 10 |
(1)�����������ϵ���Ϊ3��Ƶ�ʼ��������ϵ���Ϊ5��Ƶ�ʣ�
(2)��ǿ˵����������������֪һ�������г������ϵ���Ϊ5�ĸ��������������˵���������540������ô�������ϵ���Ϊ6�Ĵ���������100���������ж���ǿ������˵���ĶԴ���