题目内容
【题目】如图,∠MON=90°,点A、B分别在边ON和OM上(∠OAB≠45°).

(1)根据要求,利用尺规作图,补全图形:
第①步:作∠MON的平分线OC,作线段AB的垂直平分线l,OC和l交于点P,第②步:连接PA、PB;
(2)结合补完整的图形,判断PA和PB有什么数量关系和位置关系?并说明理由.
【答案】(1)见详解;(2)AP=BP,AP⊥BP,理由见详解.
【解析】
(1)利用尺规作图的方法,作出∠MON的平分线OC,作线段AB的垂直平分线l,OC和l交于点P,连接PA、PB;
(2)由垂直平分线定理,得到AP=BP;作PD⊥ON与D,PE⊥OM与E,由点P在OC上,则PD=PE,即可证明Rt△ADP≌Rt△BEP,则∠APD=∠BPE,由∠DPE=90°,得到∠APB=90°,然后得到AP⊥BP.
解:(1)如图所示;
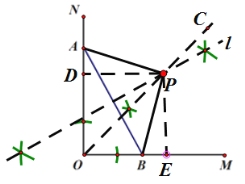
(2)AP=BP,AP⊥BP;
理由如下:
∵直线l垂直平分AB,点P在l上,
∴AP=BP;
如上图,作PD⊥ON与D,PE⊥OM与E,
∵点P在∠MON的平分线OC上,
∴PD=PE,
∴Rt△ADP≌Rt△BEP(HL),
∴∠APD=∠BPE;
∵∠MON=90°,PD⊥ON,PE⊥OM,PD=PE,
∴四边形OEPD是正方形;
∴∠DPE=90°,
∴∠APD+∠DPB=∠DPB+∠BPE=∠DPE=90°,
∴∠APB=90°,
∴AP⊥BP.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目