Question

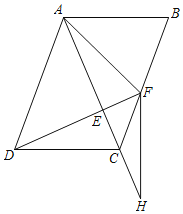
【题目】如图，在平行四边形ABCD中，连接AC，AD＝AC，过点D作DF⊥AC交BC于点F，交AC于点E，连接AF．

（1）若AE＝4，DE＝2EC，求EC的长．

（2）延长AC至点H，连接FH，使∠H＝∠EDC，若AB＝AF＝FH，求证：FD+FC＝AD．

Answer 1

【答案】（1）EC＝；（2）详见解析．

【解析】

（1）设EC＝x，则DE＝2x，AD＝AC＝AE+EC＝4+x，在Rt△ADE中，由勾股定理得出方程，解方程即可；

（2）证明△DEC≌△HEF（AAS），得出EC＝EF，DE＝EH，得出△CEF是等腰直角三角形，得出∠ECF＝45°，再证明△ADE是等腰直角三角形，得出∠DAC＝45°，DE＝AD，由等腰三角形的性质得出∠ADC＝∠ACD＝67.5°，求出∠EDC＝∠H＝22.5°，得出∠CFH＝∠EF﹣∠H＝22.5°＝∠H，证出CF＝CH，即可得出结论．

（1）解：设EC＝x，则DE＝2x，AD＝AC＝AE+EC＝4+x，

∵DF⊥AC，

∴∠AED＝90°，

在Rt△ADE中，由勾股定理得：（2x）2+42＝（4+x）2，

解得：x＝，或x＝0（舍去），

∴EC＝；

（2）证明：∵四边形ABCD是平行四边形，

∴AB＝CD，

∵AB＝AF＝FH，

∴CD＝FH，

∵DF⊥AC，

∴∠DEC＝∠HEF＝90°，

在△DEC和△HEF中，，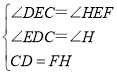

∴△DEC≌△HEF（AAS），

∴EC＝EF，DE＝EH，

∵DF⊥AC，

∴△CEF是等腰直角三角形，

∴∠ECF＝45°，

∵AF＝FH，DF⊥AC，

∴AE＝HE＝DE，

∴△ADE是等腰直角三角形，

∴∠DAC＝45°，DE＝AD，

∵AD＝AC，

∴∠ADC＝∠ACD＝（180°﹣45°）＝67.5°，

∴∠EDC＝∠H＝22.5°，

∴∠CFH＝∠EF﹣∠H＝22.5°＝∠H，

∴CF＝CH，

∴EF+FC＝EC+CH＝EH＝DE，

∴FD+FC＝DE+EF+FC＝DE+DE＝2DE＝AD．