��Ŀ����
����Ŀ����֪��ABD����GDF���ǵ���ֱ�������Σ�BD��DF��Ϊб�ߣ�BD��DF����
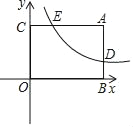
��1����ͼ1��B��D��F��ͬһֱ���ϣ���F��MF��GF�ڵ�F��ȡMF=AB������AM��BF�ڵ�H������GA��GM��
����֤��AH=HM��
�����ж���GAM����״��������֤����
�����õ�ʽ��ʾ�߶�AM��BD��DF��������ϵ����˵�����ɣ�
��2����ͼ2��GD��BD������BF��ȡBF���е�H������AH���ӳ���DF�ڵ�M�����õ�ʽֱ��д���߶�AM��BD��DF��������ϵ��

���𰸡���1��������������������������2��AM2=BD2+DF2��![]() DFBD��
DFBD��
��������
��1������֤��ABD=��HFM=45�����Ӷ����ݡ�AAS����֤��AHB�ա�MHF����ȫ�������εĶ�Ӧ����ȿɵ�AH=HM��
�ڸ��ݡ�SAS����֤��GAD�ա�GMF���Ӷ�AG=GM����AGD=��MGF��������֤��AGM=90��,������GAM�ǵ���ֱ����������
�۸��ݹ��ɶ������ɵó��߶�AM��BD��DF��������ϵ��
��2����֤��ADM=90�������ݡ�AAS����֤��ABH�ա�HFM���Ӷ�FM=AB��Ȼ�����AM2=AD2+DM2��������.
��1����֤������ͼ1����MF��GF��
���GFM=90�㣬
�ߡ�ABD����GDF���ǵ���ֱ�������Σ�
���DFG=��ABD=45�㣬
���HFM=90�㩁45��=45�㣬
���ABD=��HFM��
��AB=MF����AHB=��MHF��
���AHB�ա�MHF��
��AH=HM��
����ͼ1����GAM�ǵ���ֱ�������Σ������ǣ�
�ߡ�ABD����GDF���ǵ���ֱ�������Σ�
��AB=AD��DG=FG��
��ADB=��GDF=45�㣬
���ADG=��GFM=90�㣬
��AB=FM��
��AD=FM��
���GAD�ա�GMF��
��AG=GM����AGD=��MGF��
���ADG+��DGM=��MGF+��DGM=90�㣬
���GAM�ǵ���ֱ�������Σ�
����ͼ1��AM2=BD2+DF2�������ǣ�
�ߡ�AGM�ǵ���ֱ�������Σ�
��AM2=2MG2��
Rt��GMF��MG2=FG2+FM2=AB2+FG2��
�ߡ�ABD����GDF���ǵ���ֱ�������Σ�
��AB=![]() ��FG=
��FG=![]() ��
��
��AM2=2MG2=2��![]() +
+![]() ��=BD2+DF2��
��=BD2+DF2��
��2����ͼ2����GD��BD����ADB=45�㣬
���ADG=45�㣬
���ADM=45��+45��=90�㣬
�ߡ�HMF=��ADM+��DAM=90��+��DAM=��BAH��
��H��BF���е㣬
��BH=HF��
�ߡ�AHB=��MHF��
���ABH�ա�HFM��
��FM=AB��
��Rt��ADM�У��ɹ��ɶ����ã�AM2=AD2+DM2��
=AD2+��DF��FM��2��
=AD2+DF2��2DFFM+FM2��
=BD2+DF2��2DF![]() ��
��
=BD2+DF2��![]() DFBD��
DFBD��

 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д�