题目内容
【题目】如图,Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE.

(1)如图1,过F点作FD⊥AC交AC于D点,求证:EC+CD=DF;
(2)如图2,连接BF交AC于G点,若![]() =3,求证:E点为BC中点;
=3,求证:E点为BC中点;
(3)当E点在射线CB上,连接BF与直线AC交于G点,若![]() ,则
,则![]() =_______
=_______
【答案】(1)答案见解析;(2)答案见解析;(3)![]() .
.
【解析】
(1)通过全等三角形△ADF≌△EDA的对应边相等得到:AD=CD,FD=AC,则利用等量代换和图形中相关线段间的和差关系证得结论;
(2)过F点作FD⊥AC交AC于D点,根据(1)中结论可得FD=AC=BC,即可证明△FGD≌△BCD,可得DG=CG,根据![]() =3可证
=3可证![]() ,根据AD=CE,AC=BC,即可解题;(3)过F作FD⊥AG的延长线交于点D,易证
,根据AD=CE,AC=BC,即可解题;(3)过F作FD⊥AG的延长线交于点D,易证![]() ,由(1)(2)可知△ADF≌△ECA,△GDF≌△GCB,可得CG=GD,AD=CE,即可求得
,由(1)(2)可知△ADF≌△ECA,△GDF≌△GCB,可得CG=GD,AD=CE,即可求得![]() 的值,即可解题.
的值,即可解题.
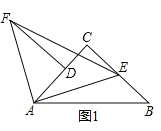
证明:(1)如图1,∵∠FAD+∠CAE=90°,∠FAD+∠F=90°,
∴∠CAE=∠AFD,
在△ADF和△ECA中,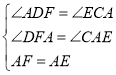 ,
,
∴△ADF≌△ECA(AAS),
∴AD=CD,FD=AC,
∴CE+CD=AD+CD=AC=FD,即EC+CD=DF;
证明:(2)如图2,
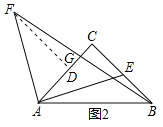
过F点作FD⊥AC交AC于D点,
∵△ADF≌△ECA,
∴FD=AC=BC,
在△FDG和△BCG中,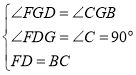 ,
,
∴△FDG≌△BCG(AAS),
∴GD=CG,
∵![]() =3
=3
∴![]()
∴![]() ,
,
∵AD=CE,AC=BC
∴![]() ,
,
∴E点为BC中点;
(3)过F作FD⊥AG的延长线交于点D,如图3,
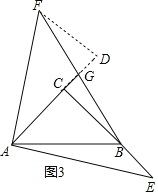
∵![]() ,BC=AC,CE=CB+BE,
,BC=AC,CE=CB+BE,
∴![]() ,
,
由(1)(2)知:△ADF≌△ECA,△GDF≌△GCB,
∴CG=GD,AD=CE,
∴![]() ,
,
∴![]() .
.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案