题目内容
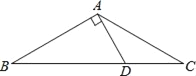
【题目】如图,在△ABC中,∠C=∠ABC,BE⊥AC,垂足为点E,△BDE是等边三角形,若AD=4,则线段BE的长为______.

【答案】4
【解析】
本题首先由等边三角形的性质及垂直定义得到∠DBE=60°,∠BEC=90°,再根据等腰三角形的性质可以得出∠EBC=∠ABC-60°=∠C-60°,最后根据三角形内角和定理得出关系式∠C-60°+∠C=90°解出∠C,推出AD=DE,于是得到结论.
∵△BDE是正三角形,
∴∠DBE=60°;
∵在△ABC中,∠C=∠ABC,BE⊥AC,
∴∠C=∠ABC=∠ABE+∠EBC,则∠EBC=∠ABC-60°=∠C-60°,∠BEC=90°;
∴∠EBC+∠C=90°,即∠C-60°+∠C=90°,
解得∠C=75°,
∴∠ABC=75°,
∴∠A=30°,
∵∠AED=90°-∠DEB=30°,
∴∠A=∠AED,
∴DE=AD=4,
∴BE=DE=4,
故答案为:4.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别(m) | 频数 |
1.09~1.19 | 8 |
1.19~1.29 | 12 |
1.29~1.39 | A |
1.39~1.49 | 10 |
(1)求a的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.