题目内容
如图,矩形ABCD∽矩形AFEB,若S矩形ABCD:S矩形AFEB=9:16,AB=6,则S矩形ABCD的值为()
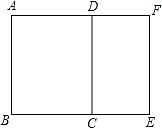

| A.9 | B.16 | C.27 | D.48 |
C.
试题分析:先根据矩形ABCD∽矩形AFEB,若S矩形ABCD:S矩形AFEB=9:16得出
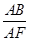 的值,再由AB=6可求出AF的长,进而可得出结论.
的值,再由AB=6可求出AF的长,进而可得出结论.解答:解:∵矩形ABCD∽矩形AFEB,S矩形ABCD:S矩形AFEB=9:16,
∴
 ,
,∵AB=6,
∴AF=8,
∴S矩形AFEBF=6×8=48,
∴S矩形ABCD=48×
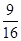 =27.
=27.故选C.
考点:相似多边形的性质.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
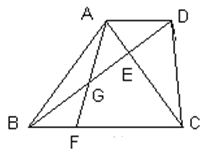
 。
。
 ,求证:
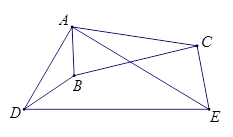
,求证: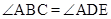 .
. 
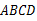 中,
中,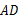 ∥
∥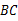 ,点
,点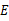 是边
是边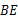 交
交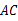 于
于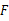 ,
, 的延长线于
的延长线于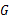 .
.
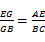 ;(2)若
;(2)若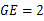 ,
,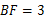 ,求线段
,求线段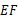 的长.
的长.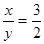 ,则
,则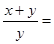 .
.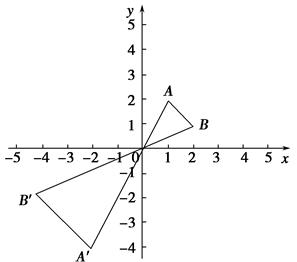
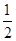 ,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )
,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )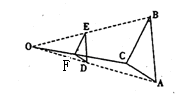
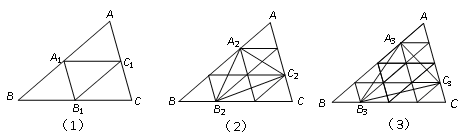
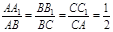 , 则
, 则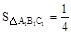 ;
;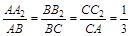 , 则
, 则 ;
; , 则
, 则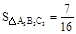 ;
;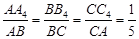 , 则
, 则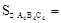
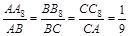 , 则
, 则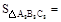 .
.