题目内容
如图,已知△ABC的面积S△ABC=1.
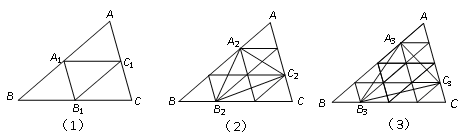
在图(1)中,若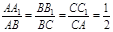 , 则
, 则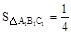 ;
;
在图(2)中,若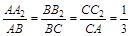 , 则
, 则 ;
;
在图(3)中,若 , 则
, 则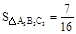 ;
;
按此规律,若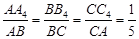 , 则
, 则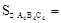
若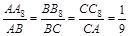 , 则
, 则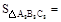 .
.

在图(1)中,若
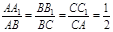 , 则
, 则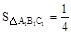 ;
;在图(2)中,若
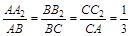 , 则
, 则 ;
;在图(3)中,若
 , 则
, 则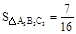 ;
;按此规律,若
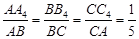 , 则
, 则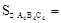
若
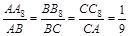 , 则
, 则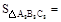 .
.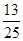 ;
;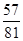 .
.试题分析:求得三角形ABC的面积S与对应边的比值之间的函数关系,然后代入比值求函数值即可.
设函数关系为S=ax2+bx+c,
∵若
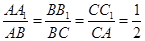 ,则S△A1B1C1=
,则S△A1B1C1=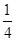 ;若
;若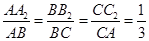 ,则S△A1B1C1=
,则S△A1B1C1=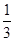 ;
;若
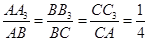 ,则S△A1B1C1=
,则S△A1B1C1=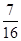 ;
;∴
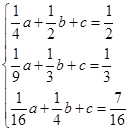
解得:a=3,b=-3,c=1
∴S=3x2-3x+1
∴若
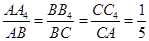 ,则S△A1B1C1=3×(
,则S△A1B1C1=3×(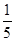 )2-3×
)2-3×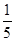 +1=
+1=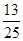 ;
;若
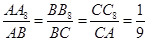 ,则S△A1B1C1=3×(
,则S△A1B1C1=3×(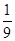 )2-3×
)2-3×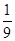 +1=
+1=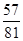 .
.考点: 1.规律型:图形的变化类;2.三角形的面积.

练习册系列答案
相关题目


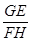 的值.
的值. 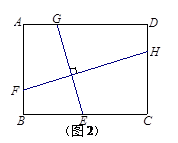
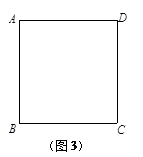
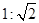
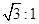
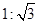
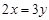 ,那么
,那么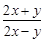 = .
= .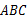 三个顶点的坐标分别为
三个顶点的坐标分别为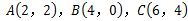 ,以原点为位似中心,将△
,以原点为位似中心,将△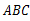 缩小,位似比为
缩小,位似比为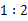 ,则线段
,则线段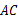 的中点
的中点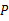 变换后对应点的坐标为_________.
变换后对应点的坐标为_________. 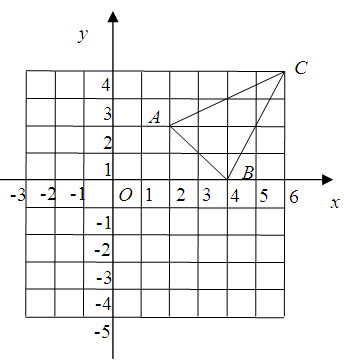
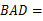 ∠
∠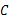 ,
,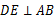 于
于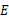 ,
, 于
于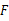 ,若
,若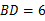 ,
,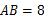 ,则
,则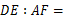 ______.
______.