题目内容
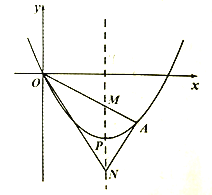
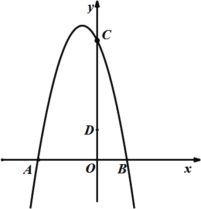
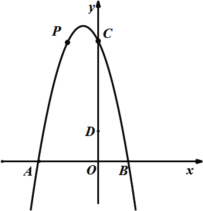
【题目】如图1,由于四边形具有不稳定性,因此在同一平面推矩形的边可以改变它的形状(推移过程中边的长度保持不变).已知矩形ABCD,AB=4cm,AD=3cm,固定边AB,推边AD,使得点D落在点E处,点C落在点F处.
(1)如图2,如果∠DAE=30°,求点E到边AB的距离;
(2)如图3,如果点A、E、C三点在同一直线上,求四边形ABFE的面积.
【答案】(1)点E到边AB的距离是![]() cm;(2)
cm;(2)![]()
【解析】
(1)过点E作EH⊥AB轴,垂足为H,根据矩形的性质得到∠DAB=90°,AD∥EH,根据平行线的性质得到∠DAE=∠AEH,求得∠AEH=30°,解直角三角形即可得到结论;
(2)过点E作EH⊥AB,垂足为H.根据矩形的性质得到AD=BC.得到BC=3cm.根据勾股定理得到![]() cm,根据平行线分线段成比例定理得到
cm,根据平行线分线段成比例定理得到![]() cm,根据四边形的性质得到AD=AE=BF,AB=DC=EF.求得四边形ABFE是平行四边形,于是得到结论.
cm,根据四边形的性质得到AD=AE=BF,AB=DC=EF.求得四边形ABFE是平行四边形,于是得到结论.
解:(1)如图,过点E作EH⊥AB轴,垂足为H,
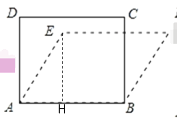
∵四边形ABCD是矩形,
∴∠DAB=90°,
∴AD∥EH,
∴∠DAE=∠AEH,
∵∠DAE=30°,
∴∠AEH=30°.
在直角△AEH中,∠AHE=90°,
∴EH=AEcos∠AEH,
∵AD=AE=3cm,
∴![]() cm,
cm,
即点E到边AB的距离是![]() cm;
cm;
(2)如图3,过点E作EH⊥AB,垂足为H.
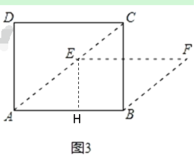
∵四边形ABCD是矩形,
∴AD=BC,
∵AD=3cm,
∴BC=3cm,
在直角△ABC中,∠ABC=90°,AB=4cm,
∴![]() cm,
cm,
∵EH∥BC,
∴![]() ,
,
∵AE=AD=3 cm,
∴![]() ,
,
∴![]() cm,
cm,
∵推移过程中边的长度保持不变,
∴AD=AE=BF,AB=DC=EF,
∴四边形ABFE是平行四边形,
∴![]() cm2.
cm2.

练习册系列答案
相关题目