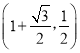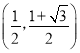题目内容
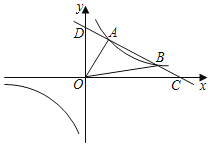
【题目】在平面直角坐标系中,点![]() 与
与![]()
![]() 称为一对泛对称点.
称为一对泛对称点.
(1)若点![]() ,
,![]() 是一对泛对称点,求
是一对泛对称点,求![]() 的值;
的值;
(2)若![]() ,
,![]() 是第一象限的一对泛对称点,过点
是第一象限的一对泛对称点,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,线段
,线段![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() ,判断直线
,判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)抛物线![]()
![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交此抛物线于点
轴的平行线交此抛物线于点![]() (不与点
(不与点![]() 重合),过点
重合),过点![]() 的直线
的直线![]() 与此抛物线交于另一点
与此抛物线交于另一点![]() .对于任意满足条件的实数
.对于任意满足条件的实数![]() ,是否都存在
,是否都存在![]() ,
,![]() 是一对泛对称点的情形?若是,请说明理由,并对所有的泛对称点
是一对泛对称点的情形?若是,请说明理由,并对所有的泛对称点![]() ,
,![]() 探究当
探究当![]() >
>![]() 时
时![]() 的取值范围;若不是,请说明理由.
的取值范围;若不是,请说明理由.
【答案】(1)![]() ;(2)AB∥PQ,见解析;(3)对于任意满足条件的实数b,都存在M,N是一对泛对称点的情形,此时对于所有的泛对称点M(xM,yM),N(xN,yN),当yM>yN时,xM的取值范围是xM<1且xM≠0
;(2)AB∥PQ,见解析;(3)对于任意满足条件的实数b,都存在M,N是一对泛对称点的情形,此时对于所有的泛对称点M(xM,yM),N(xN,yN),当yM>yN时,xM的取值范围是xM<1且xM≠0
【解析】
(1)利用泛对称点得定义求出t的值,即可求出a.
(2)设P,Q两点的坐标分别为P(p,tq),Q(q,tp),根据题干条件得到A(p,0),B(0,tp),C(p,tp)的坐标,利用二元一次方程组证出k1=k2,所以AB∥PQ.
(3)由二次函数与x轴交点的特征,得到D点的坐标;然后利用二次函数与一元二次方程的关系,使用求根公式即可得到答案.
(1)解:因为点(1,2),(3,a)是一对泛对称点,
设3t=2
解得t=![]()
所以a=t×1=![]()
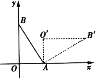
(2)解:设P,Q两点的坐标分别为P(p,tq),Q(q,tp),其中0<p<q,t>0.
因为PA⊥x轴于点A,QB⊥y轴于点B,线段PA,QB交于点C,
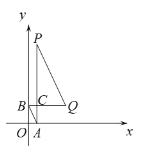
所以点A,B,C的坐标分别为:A(p,0),B(0,tp),C(p,tp)
设直线AB,PQ的解析式分别为:y=k1x+b1,y=k2x+b2,其中k1k2≠0.
分别将点A(p,0),B(0,tp)代入y=k1x+b1,得
 . 解得
. 解得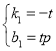
分别将点P(p,tq),Q(q,tp)代入y=k2x+b2,得
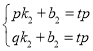 . 解得
. 解得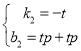
所以k1=k2.
所以AB∥PQ
(3)解:因为抛物线y=ax2+bx+c(a<0)交y轴于点D,
所以点D的坐标为(0,c).
因为DM∥x轴,
所以点M的坐标为(xM,c),又因为点M在抛物线y=ax2+bx+c(a<0)上.
可得axM 2+bxM+c=c,即xM(axM+b)=0.
解得xM=0或xM=-![]() .
.
因为点M不与点D重合,即xM≠0
所以点M的坐标为(-![]() ,c)
,c)
因为直线y=ax+m经过点M,
将点M(-![]() ,c)代入直线y=ax+m可得,a·(-
,c)代入直线y=ax+m可得,a·(-![]() )+m=c.
)+m=c.
化简得m=b+c
所以直线解析式为:y=ax+b+c.
因为抛物线y=ax2+bx+c与直线y=ax+b+c交于另一点N,
由ax2+bx+c=ax+b+c,可得ax2+(b-a)x-b=0.
因为△=(b-a)2+4ab=(a+b)2,
解得x1=-![]() ,x2=1.
,x2=1.
即xM=-![]() ,xN=1,且-
,xN=1,且-![]() ≠1,也即a+b≠0.
≠1,也即a+b≠0.
所以点N的坐标为(1,a+b+c)
要使M(-![]() ,c)与N(1,a+b+c)是一对泛对称点,
,c)与N(1,a+b+c)是一对泛对称点,
则需c=t ×1且a+b+c=t ×(-![]() ).
).
也即a+b+c=(-![]() )·c
)·c
也即(a+b)·a=-(a+b)·c.
因为a+b≠0,
所以当a=-c时,M,N是一对泛对称点.
因此对于任意满足条件的实数b,都存在M,N是一对泛对称点的情形.
此时点M的坐标为(-![]() ,-a),点N的坐标为(1,b).
,-a),点N的坐标为(1,b).
所以M,N两点都在函数y=![]() (b≠0)的图象上.
(b≠0)的图象上.
因为a<0,
所以当b>0时,点M,N都在第一象限,此时 y随x的增大而减小,所以当yM>yN时,0<xM<1;
当b<0时,点M在第二象限,点N在第四象限,满足yM>yN,此时xM<0.
综上,对于任意满足条件的实数b,都存在M,N是一对泛对称点的情形,此时对于所有的泛对称点M(xM,yM),N(xN,yN),当yM>yN时,xM的取值范围是xM<1且/span>xM≠0.

 星级口算天天练系列答案
星级口算天天练系列答案【题目】如今很多初中生喜欢购头饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A.白开水,B.瓶装矿泉水,C.碳酸饮料,D.非碳酸饮料.根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题
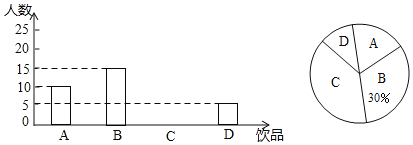
(1)这个班级有多少名同学?并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如下表),则该班同学每天用于饮品的人均花费是多少元?
饮品名称 | 白开水 | 瓶装矿泉水 | 碳酸饮料 | 非碳酸饮料 |
平均价格(元/瓶) | 0 | 2 | 3 | 4 |
(3)为了养成良好的生活习惯,班主任决定在饮用白开水的5名班委干部(其中有两位班长记为A,B,其余三位记为C,D,E)中随机抽取2名班委干部作良好习惯监督员,请用列表法或画树状图的方法求出恰好抽到2名班长的概率.