题目内容
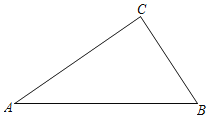
【题目】(解决问题)已知![]() ,
,![]() ,
,![]() 是同一平面上的三个点,以线段
是同一平面上的三个点,以线段![]() ,
,![]() 为边,分别作正三角形
为边,分别作正三角形![]() 和正三角形
和正三角形![]() ,连接
,连接![]() ,
,![]() .
.
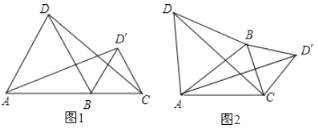
(1)如图1,当点![]() ,
,![]() ,
,![]() 在同一直线上时,线段
在同一直线上时,线段![]() 与
与![]() 的大小关系是__________;
的大小关系是__________;
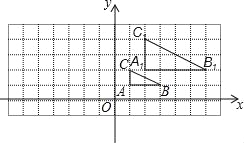
(2)如图2,当![]() ,
,![]() ,
,![]() 为三角形的顶点时(点
为三角形的顶点时(点![]() ,
,![]() ,
,![]() 不在同一条直线上),判断线段
不在同一条直线上),判断线段![]() 与
与![]() 的大小关系是否发生改变,并说明理由;
的大小关系是否发生改变,并说明理由;
(类比猜想)
(3)已知![]() ,
,![]() ,
,![]() 是同一平面上的三个点,以线段
是同一平面上的三个点,以线段![]() ,
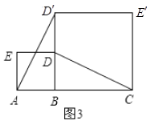
,![]() 为边,分别作正方形,连接
为边,分别作正方形,连接![]() ,
,![]() ,如图3和图4所示.判断线段
,如图3和图4所示.判断线段![]() 与
与![]() 的大小关系,并在图4(点
的大小关系,并在图4(点![]() ,
,![]() ,
,![]() 不在同一条直线上)中证明你的判断;
不在同一条直线上)中证明你的判断;
(推广应用)(4)上面的这些结论能否推广到任意正多边形(不必证明)?
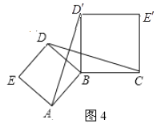
(5)如图5,![]() 与
与![]() 的大小关系是__________,并写出它们分别在哪两个全等三角形中;
的大小关系是__________,并写出它们分别在哪两个全等三角形中;
(6)请在图6中连接图中两个顶点,构造处一组全等三角形,并写出这两个全等的三角形.

【答案】(1)相等;(2)没有发生变化,理由见解析;(3)![]() =
=![]() ,理由见解析;(4)能推广到任意正多边形;(5)相等;△ABD’≌△DBC;(6)△GAD’≌△BAC.
,理由见解析;(4)能推广到任意正多边形;(5)相等;△ABD’≌△DBC;(6)△GAD’≌△BAC.
【解析】
(1)根据正三角形的性质证明△ABD’≌△DBC,即可求解;
(2)同理证明△ABD’≌△DBC,即可求解;
(3)根据正方形的性质同理证明△ABD’≌△DBC,即可求解;
(4)根据题意及图形的特点可知这些结论能否推广到任意正多边形;
(5)根据正五边形的性质同理证明△ABD’≌△DBC,即可求解;
(6)连接GD’,证明△ABC≌△AGD’即可求解.
(1)∵△ABD、△BCD’是等边三角形,
∴AB=BD,BD’=BC, ![]()
∵![]() ,
,![]()
∴![]()
∴△ABD’≌△DBC(SAS)
∴![]() =
=![]()
故答案为:相等;
(2)线段![]() 与
与![]() 的大小关系没有改变,理由如下:
的大小关系没有改变,理由如下:
∵△ABD、△BCD’是等边三角形,
∴AB=BD,BD’=BC, ![]()
∵![]() ,
,![]()
∴![]()
∴△ABD’≌△DBC(SAS)
∴![]() =
=![]()
(3)在如图3和图4.判断线段![]() 与
与![]() 的大小关系为相等,理由如下:
的大小关系为相等,理由如下:
∵四边形ABDE、四边形BCD’E’是正方形,
∴AB=BD,BD’=BC, ![]()
∵![]() ,
,![]()
∴![]()
∴△ABD’≌△DBC(SAS)
∴![]() =
=![]()
故线段![]() 与
与![]() 的大小关系为相等;
的大小关系为相等;
(4)根据题意及图形的特点同理可得△ABD’≌△DBC,则![]() =
=![]()
故线段![]() 与
与![]() 的大小关系为相等,能推广到任意正多边形;
的大小关系为相等,能推广到任意正多边形;
(5)∵五边形ABDEF、五边形BCF’E’ D’是正方形,
∴AB=BD,BD’=BC, ![]()
∵![]() ,
,![]()
∴![]()
∴△ABD’≌△DBC(SAS)
∴![]() =
=![]()
故答案为:相等;△ABD’≌△DBC;
(6)如图,连接GD’,
∵六边形ABDEFG、六边形ACG’F’E’ D’是正方形,
∴AB=AG,AD’=AC, ![]()
∵![]() ,
,![]()
∴![]()
∴△GAD’≌△BAC(SAS)
故答案为△GAD’≌△BAC.